题目内容
2．
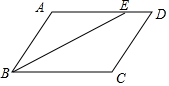如图，在平行四边形ABCD中，∠ABC的平分线BE交AD于E，∠AEB=25°，则∠A的大小为（ ）| A． | 100° | B． | 120° | C． | 130° | D． | 150° |
分析 由平行四边形的性质得出∠AEB=∠CBE，由角平分线的定义和邻补角关系得出∠ABE=∠CBE=∠AEB=25°，再由三角形内角和定理即可得出∠A的度数．
解答 解：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠AEB=∠CBE，
∵∠ABC的平分线交AD于E，
∴∠ABE=∠CBE=∠AEB=25°，
∴∠A=180°-∠ABE-∠AEB=130°．
故选：C．
点评 本题考查了平行四边形的性质、三角形内角和定理；熟练掌握平行四边形的性质，求出∠ABE=∠CBE=∠AEB是解决问题的关键．
练习册系列答案
相关题目
13．方程组$\left\{\begin{array}{l}{x+y=3}\\{x-y=-1}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=1}\\{y=-3}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$ |
已如抛物线y=ax2+bx+c与直线y=mx+n相交于两点，这两点的坐标分别是（0，-$\frac{1}{2}$）和（m-b，m2-mb+n），其中a，b，c，m，n为实数，且a，m不为0．
如图，已知△ABC的两条高BD、CE相交于点O，且OB=OC．求证：AB=AC．