题目内容
9.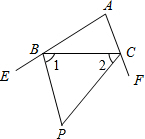 如图,BP,CP分别是∠CBE,∠BCF的平分线,求出∠P与∠A的等量关系.
如图,BP,CP分别是∠CBE,∠BCF的平分线,求出∠P与∠A的等量关系.
分析 如图,设∠ABC=α,∠ACB=β;首先运用α、β表示出∠1+∠2,进而求出∠P;其次运用α、β表示出∠A,从而探究出∠P与∠A之间的等量关系.
解答  解:如图,设∠ABC=α,∠ACB=β;∵
解:如图,设∠ABC=α,∠ACB=β;∵
BP,CP分别是∠CBE,∠BCF的平分线,
∴∠1=$\frac{180°-α}{2}$,∠2=$\frac{180°-β}{2}$,
∴∠1+∠2=180°-$\frac{1}{2}$(α+β),
∴∠P=180°-[180°-$\frac{1}{2}$(α+β)]=$\frac{1}{2}$(α+β);
∵∠A=180°-(α+β),
∴∠P=90°-$\frac{1}{2}$∠A.
点评 该题主要考查了三角形的内角和定理、外角的性质等知识点及其应用问题;解题的关键是能够灵活运用三角形的内角和定理、外角的性质等知识点来分析、判断、解答.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
20.下列计算正确的个数是( )
①(x+y)2=x2+y2
②(-x+y)2=x2-2xy+y2
③(x+2y)(x-2y)=x2-2y2
④(-2a-3)(2a-3)=9-4a2
⑤(a-b)2=a2-b2.
①(x+y)2=x2+y2
②(-x+y)2=x2-2xy+y2
③(x+2y)(x-2y)=x2-2y2
④(-2a-3)(2a-3)=9-4a2
⑤(a-b)2=a2-b2.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
4.下列等式成立的是( )
| A. | (a+b)2=a2+b2 | B. | (a-b)2=a2-b2 | C. | (x-4)(x+4)=x2-4 | D. | (a+b)2=a2+b2+2ab |
14.已知甲处看乙处为仰角30°,则乙处看甲处为( )
| A. | 仰角30° | B. | 俯角30° | C. | 仰角60° | D. | 俯角60° |
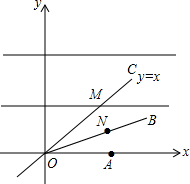 如图点A(2,0)点N在射线OB上运动,点M是直线y=x上一动点,OB为∠AOC的角平分线,求AN+MN的最小值,要画出图象.
如图点A(2,0)点N在射线OB上运动,点M是直线y=x上一动点,OB为∠AOC的角平分线,求AN+MN的最小值,要画出图象.