题目内容
17.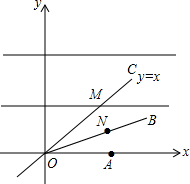 如图点A(2,0)点N在射线OB上运动,点M是直线y=x上一动点,OB为∠AOC的角平分线,求AN+MN的最小值,要画出图象.
如图点A(2,0)点N在射线OB上运动,点M是直线y=x上一动点,OB为∠AOC的角平分线,求AN+MN的最小值,要画出图象.
分析 过AM⊥OC于M,交OB于N,此时AN+MN=AM,根据垂线段最短可知AM就是AN+MN的最小值;因为点M是直线y=x上一动点,求得∠AOC=45°,得出△AOM是等腰直角三角形,解等腰直角三角形即可求得AM.
解答 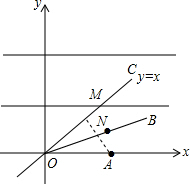 解:过AM⊥OC于M,交OB于N,此时AN+MN=AM,根据垂线段最短可知AM就是AN+MN的最小值.
解:过AM⊥OC于M,交OB于N,此时AN+MN=AM,根据垂线段最短可知AM就是AN+MN的最小值.
∵点M是直线y=x上一动点,
∴∠AOC=45°,
∵AM⊥OC,
∴△AOM是等腰直角三角形,
∵点A(2,0),
∴OA=2,
∴AM=OM=$\sqrt{2}$,
∴AN+MN的最小值为$\sqrt{2}$.
点评 本题是直角三角形和对称的性质的综合应用,正确确定AN+MN最小的条件是本题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
12.在Rt△ABC中,∠C=90°,sinA=$\frac{5}{13}$,则tanA的值为( )
| A. | $\frac{12}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{13}{12}$ | D. | $\frac{12}{5}$ |
2.如果一个多边形的每一个外角都比相邻内角小60°,则这个多边形是几边形( )
| A. | 6 | B. | 7 | C. | 8 | D. | 12 |
 如图,将边长为3的正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
如图,将边长为3的正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.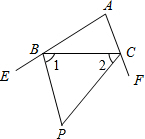 如图,BP,CP分别是∠CBE,∠BCF的平分线,求出∠P与∠A的等量关系.
如图,BP,CP分别是∠CBE,∠BCF的平分线,求出∠P与∠A的等量关系.