题目内容
19.若a、b均为整数,当x=$\sqrt{3}$-1时,代数式x2+ax+b的值为0,求$\frac{1}{{b}^{a}}$的算术平方根.分析 把x的值代入代数式,使其值为0,根据a,b均为整数,求出a与b的值,代入原式计算,求出算术平方根即可.
解答 解:当x=$\sqrt{3}$-1时,代数式x2+ax+b的值为0,
可得4-2$\sqrt{3}$+($\sqrt{3}$-1)a+b=0,即(a-2)$\sqrt{3}$+4-a+b=0,
∵a,b均为整数,
∴a-2=0,4-a+b=0,
解得:a=2,b=-2,
则$\frac{1}{{b}^{a}}$=$\frac{1}{(-2)^{2}}$=$\frac{1}{4}$,其算术平方根为$\frac{1}{2}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.某次数学考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我组成绩是87分的同学最多.”小英说:“我们组的7位同学成绩排在最中间的恰好也是87分.”上面两位同学的话能反映的统计量是( )
| A. | 众数和平均数 | B. | 平均数和中位数 | C. | 众数和方差 | D. | 众数和中位数 |
11.直线y=x-2不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,将边长为3的正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
如图,将边长为3的正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.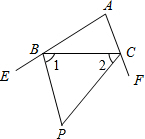 如图,BP,CP分别是∠CBE,∠BCF的平分线,求出∠P与∠A的等量关系.
如图,BP,CP分别是∠CBE,∠BCF的平分线,求出∠P与∠A的等量关系.