题目内容
在平面直角坐标系中,抛物线y=-
x2+
mx+m2-3m+2与x轴的交点分别为原点O和点A,点B(4,n)在这条抛物线上.
(1)求B点的坐标;
(2)将此抛物线的图象向上平移
个单位,求平移后的图象的解析式;
(3)在(2)的条件下,将平移后的二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线y=
x+b与此图象有两个公共点时,b的取值范围.
| m-1 |
| 2 |
| 3 |
| 2 |
(1)求B点的坐标;
(2)将此抛物线的图象向上平移
| 7 |
| 2 |
(3)在(2)的条件下,将平移后的二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线y=
| 1 |
| 2 |
考点:二次函数综合题
专题:压轴题
分析:(1)把原点坐标代入抛物线,解关于m的一元二次方程得到m的值,再根据二次项系数不等于0确定出函数解析式,再把点B坐标代入函数解析式求出n的值,即可得解;
(2)根据向上平移纵坐标加解答即可;
(3)把直线解析式与抛物线解析式联立,消掉y得到关于x的一元二次方程,根据△=0求出b的值,然后令y=0求出抛物线与x轴的交点坐标,再求出直线经过抛物线与x轴左边交点的b值,然后根据图形写出b的取值范围即可.
(2)根据向上平移纵坐标加解答即可;
(3)把直线解析式与抛物线解析式联立,消掉y得到关于x的一元二次方程,根据△=0求出b的值,然后令y=0求出抛物线与x轴的交点坐标,再求出直线经过抛物线与x轴左边交点的b值,然后根据图形写出b的取值范围即可.
解答:解:(1)∵抛物线经过原点O,
∴m2-3m+2=0,
解得m1=1,m2=2,
当m=1时,-
=-
=0,
∴m=2,
∴抛物线的解析式为y=-
x2+3x,
∵点B(4,n)在这条抛物线上,
∴n=-
×42+3×4=-8+12=4,
∴点B(4,4);
(2)∵抛物线的图象向上平移
个单位,
∴平移后的图象的解析式y=-
x2+3x+
;
(3)联立
,
消掉y得,-
x2+3x+
=
x+b,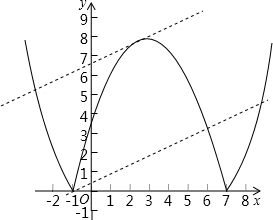
整理得,x2-5x+2b-7=0,
△=(-5)2-4×1×(2b-7)=0,
解得b=
,
令y=0,则-
x2+3x+
=0,
整理得,x2-6x-7=0,
解得x1=-1,x2=7,
∴抛物线与x轴左边的交点为(-1,0),
当直线y=
x+b经过点(-1,0)时,
×(-1)+b=0,
解得b=
,
当该直线经过点(7,0)时,
×7+b=0,
解得b=-
,
∴当直线y=
x+b与此图象有两个公共点时,b的取值范围为b>
或-
<b<
.
∴m2-3m+2=0,
解得m1=1,m2=2,
当m=1时,-
| m-1 |
| 2 |
| 1-1 |
| 2 |
∴m=2,
∴抛物线的解析式为y=-
| 1 |
| 2 |
∵点B(4,n)在这条抛物线上,
∴n=-
| 1 |
| 2 |
∴点B(4,4);
(2)∵抛物线的图象向上平移
| 7 |
| 2 |
∴平移后的图象的解析式y=-
| 1 |
| 2 |
| 7 |
| 2 |
(3)联立
|
消掉y得,-
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |

整理得,x2-5x+2b-7=0,
△=(-5)2-4×1×(2b-7)=0,
解得b=
| 53 |
| 8 |
令y=0,则-
| 1 |
| 2 |
| 7 |
| 2 |
整理得,x2-6x-7=0,
解得x1=-1,x2=7,
∴抛物线与x轴左边的交点为(-1,0),
当直线y=
| 1 |
| 2 |
| 1 |
| 2 |
解得b=
| 1 |
| 2 |
当该直线经过点(7,0)时,
| 1 |
| 2 |
解得b=-
| 7 |
| 2 |
∴当直线y=
| 1 |
| 2 |
| 53 |
| 8 |
| 7 |
| 2 |
| 1 |
| 2 |
点评:本题是二次函数综合题,主要利用了解一元二次方程,二次函数图象上点的坐标特征,二次函数图象与几何变换,难点在于(3)求出直线与抛物线有三个交点时的b值,作出图形更形象直观.

练习册系列答案
相关题目
如果三角形的三边5,m,n满足(m+n)(m-n)=25,那么这个三角形是( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、无法确定 |
 幼儿园购买了一个板长AB 4m,支架OC高0.8m的翘翘板,支点O在板AB的中点.因支架过高不宜小朋友玩,故把它暂时存放在高2.4m的车库里,准备改装.现有几个小朋友把板的一端A按到地面上.
幼儿园购买了一个板长AB 4m,支架OC高0.8m的翘翘板,支点O在板AB的中点.因支架过高不宜小朋友玩,故把它暂时存放在高2.4m的车库里,准备改装.现有几个小朋友把板的一端A按到地面上. 如图,在?ABCD中,EF∥CD,EF:CD=2:3,△DEF的面积为4,则梯形EFBA的面积为
如图,在?ABCD中,EF∥CD,EF:CD=2:3,△DEF的面积为4,则梯形EFBA的面积为