题目内容
如图，在?ABCD中，EF∥CD，EF：CD=2：3，△DEF的面积为4，则梯形EFBA的面积为考点：相似三角形的判定与性质,平行四边形的性质
专题：
分析：由平行四边形的性质可知DC∥AB，所以EF∥AB，进而得到△DEF∽△DAB，由相似三角形的性质计算即可．
解答：解：∵四边形ABCD是平行四边形，
∴DC∥AB，
∵EF∥CD，
∴EF∥AB，
∴△DEF∽△DAB，
∵EF：CD=2：3，
∴EF：AB=2：3，
△DEF的面积为4，
∴S△ABC=9，
∴梯形EFBA的面积为9-4=5，
故答案为：5．
∴DC∥AB，
∵EF∥CD，
∴EF∥AB，
∴△DEF∽△DAB，
∵EF：CD=2：3，
∴EF：AB=2：3，
△DEF的面积为4，
∴S△ABC=9，
∴梯形EFBA的面积为9-4=5，
故答案为：5．
点评：本题考查了平行四边形的性质、平行线的判定、相似三角形的判定和性质，题目的综合性较强，难度不大．
练习册系列答案
相关题目
如图，PA、PB分别切⊙O于A、B，PA=10cm，C是劣弧AB上的点（不与点A、B重合），过点C的切线分别交PA、PB于点E、F．则△PEF的周长为（ ）| A、10cm | B、15cm |
| C、20cm | D、25cm |
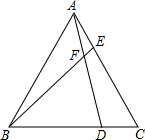如图，已知△ABC为等边三角形，点D、E分别在BC、AC边上，且AE=CD，AD与BE相交于点F．