题目内容
已知:方程
-
=
-
的解是x=
,方程
-
=
-
的解是x=
,试猜想:
(1)方程
+
=
+
的解;
(2)方程
-
=
-
的解(a、b、c、d表示不同的数).
| x-1 |
| x-2 |
| x-3 |
| x-4 |
| x-2 |
| x-3 |
| x-4 |
| x-5 |
| 7 |
| 2 |
| 1 |
| x-7 |
| 1 |
| x-5 |
| 1 |
| x-6 |
| 1 |
| x-4 |
| 11 |
| 2 |
(1)方程
| 1 |
| x-7 |
| 1 |
| x-1 |
| 1 |
| x-6 |
| 1 |
| x-2 |
(2)方程
| 1 |
| x+a |
| 1 |
| x+b |
| 1 |
| x+c |
| 1 |
| x+d |
考点:分式方程的解
专题:
分析:通过解题目中已知的两个方程的过程可以归纳出方程的解与方程中的常数之间的关系,利用这个关系可得出两个方程的解.
解答:解:
解方程
-
=
-
,先左右两边分别通分可得:
=
,
化简可得:
=
,
整理可得:2x=15-8,
解得:x=
,
这里的7即为(-3)×(-5)-(-2)×(-4),这里的2即为[-2+(-4)]-[-3+(-5)];
解方程
-
=
-
,先左右两边分别为通分可得:
=
,
化简可得:
=
,
解得:x=
,
这里的11即为(-7)×(-5)-(-4)×(-6),这里的2即为[-4+(-6)]-[-7+(-5)];
所以可总结出规律:方程解的分子为右边两个分中的常数项的积减去左边两个分母中的常数项的积,解的分母为左边两个分母中的常数项的差减去右边两个分母中常数项的差.
(1)先把方程分为两边差的形式:方程
-
=
-
,
由所总结的规律可知方程解的分子为:(-1)×(-6)-(-7)×(-2)=-8,分母为[-7+(-2)]-[-6+(-1)]=-2,所以方程的解为x=
=4;
(2)由所总结的规律可知方程解的分子为:cd-ab,分母为(a+b)-(c+d),所以方程的解为x=
.
解方程
| x-1 |
| x-2 |
| x-3 |
| x-4 |
| x-2 |
| x-3 |
| x-4 |
| x-5 |
| (x-1)(x-4)-(x-2)(x-3) |
| (x-2)(x-4) |
| (x-2)(x-5)-(x-3)(x-4) |
| (x-3)(x-5) |
化简可得:
| -1×(-4)-(-2)×(-3) |
| x2-6x+8 |
| -2×(-5)-(-3)×(-4) |
| x2-8x+15 |
整理可得:2x=15-8,
解得:x=
| 7 |
| 2 |
这里的7即为(-3)×(-5)-(-2)×(-4),这里的2即为[-2+(-4)]-[-3+(-5)];
解方程
| 1 |
| x-7 |
| 1 |
| x-5 |
| 1 |
| x-6 |
| 1 |
| x-4 |
| x-5-(x-7) |
| (x-7)(x-5) |
| x-4-(x-6) |
| (x-4)(x-6) |
化简可得:
| 2 |
| x2-12x+35 |
| 2 |
| x2-10x+24 |
解得:x=
| 11 |
| 2 |
这里的11即为(-7)×(-5)-(-4)×(-6),这里的2即为[-4+(-6)]-[-7+(-5)];
所以可总结出规律:方程解的分子为右边两个分中的常数项的积减去左边两个分母中的常数项的积,解的分母为左边两个分母中的常数项的差减去右边两个分母中常数项的差.
(1)先把方程分为两边差的形式:方程
| 1 |
| x-7 |
| 1 |
| x-2 |
| 1 |
| x-6 |
| 1 |
| x-1 |
由所总结的规律可知方程解的分子为:(-1)×(-6)-(-7)×(-2)=-8,分母为[-7+(-2)]-[-6+(-1)]=-2,所以方程的解为x=
| 8 |
| 2 |
(2)由所总结的规律可知方程解的分子为:cd-ab,分母为(a+b)-(c+d),所以方程的解为x=
| cd-ab |
| (a+b)-(c+d) |
点评:本题主要考查阅读所给知识,归纳方法规律的能力.解题的关键是由所给的两个方程总结出方程的解与已知方程中各分母中的关系.

练习册系列答案
相关题目
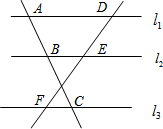 已知,如图,直线l1∥l2∥l3,若
已知,如图,直线l1∥l2∥l3,若