题目内容

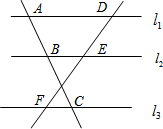已知，如图，直线l1∥l2∥l3，若
DE
DF
=
3
7
，且BC=4，求AB的长．
考点：平行线分线段成比例
专题：
分析：由平行线分线段成比例可得
DE
DF
=
AB
AC
=
3
7
，且AC=AB+BC，BC=4代入即可求得AB．
解答：解：
因为线l1∥l2∥l3，
所以若
DE
DF
=
AB
AC
=
3
7
，
且AC=AB+BC，即AC=AB+4，代入上式可得
AB
AB+4
=
3
7
，
解得AB=3．
点评：本题主要考查平行线分线段成比例的性质，解题的关键是由平行得到线段AB与已知条件中的线段之间的关系．
练习册系列答案
相关题目
已知等腰三角形底边上的高与腰上的高相等，则顶角为
 
度．
用一个正方形在某一个月份的月历上，圈出2×2这个数，这四个数的和不可能是（　　）
A、104B、112
C、24D、28
已知：方程
x-1
x-2
-
x-3
x-4
=
x-2
x-3
-
x-4
x-5
的解是x=
7
2
，方程
1
x-7
-
1
x-5
=
1
x-6
-
1
x-4
的解是x=
11
2
，试猜想：
（1）方程
1
x-7
+
1
x-1
=
1
x-6
+
1
x-2
的解；
（2）方程
1
x+a
-
1
x+b
=
1
x+c
-
1
x+d
的解（a、b、c、d表示不同的数）．
一个三角形的三边长分别为a、b、c，且关于x的方程a（x2-1）-2cx+b（x2+1）=0有两个相等实数根，判断这个三角形的形状．
设函数y=x2+px+q，根据下列条件分别确定p，q的值；                                
 （1）当x=5时，函数有最小值为-2；                                                   
 （2）函数图象与x轴的交点坐标是（-4，0）和（-1，0）．
有一个圆柱，它的高等于12cm，底面周长等于18cm，在圆柱下地面的A点有一只蚂蚁．它想吃到上底面上与A点相对B点处的食物，需要爬行最短路程是多少．（π的取值3）
解方程：y2+1.4y=1.76．
如图，AD是△ABC的边BC上的中线，E是AC边上的点，BE交AD于点G，且
AE
AC
=
3
7
，AD=6，求AG的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网