题目内容
19．
如图，已知AB=AD，若AC平分∠BAD，AC是否平分∠BCD？为什么？
分析 根据SAS证明△ABC与△ADC全等，根据全等三角形的性质即可得到结论．
解答 解：是，
理由：∵AC平分∠BAD，
∴∠BAC=∠DAC，
在△ABC与△ADC中，$\left\{\begin{array}{l}{AB=AD}\\{∠BAC=∠DAC}\\{AC=AC}\end{array}\right.$，
∴△ABC≌ADC，
∴∠ACB=∠ACD，
∴AC平分∠BCD．
点评 此题考查的是全等三角形的判定与性质，熟知全等三角形的AAS，SAS，ASA，SSS及HL定理是解答此题的关键．
练习册系列答案
相关题目
20．下列算式中，运算结果符号为正的是（ ）
| A． | 5+（-6） | B． | （-7）-（-8） | C． | -1.3+（-1.7） | D． | （-11）-7 |
如图，在四边形ABCD中，AD∥BC，∠A=90°，BC=BD，CE⊥BD，垂足为E．
如图，已知等边△ABC，AE=BD，CE，AD交于点F，过点B作BG∥CE，BG交AD的延长线于点G，求证：BG+DF=CE．
如图，△ABC的三个顶点的坐标分别是A（-2，3），B（-3，1），C（1，-2）．
6．
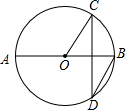如图，AB是⊙O的直径，AB=4，弦CD⊥AB，∠CDB=30°，则CD的长是（ ）
如图，AB是⊙O的直径，AB=4，弦CD⊥AB，∠CDB=30°，则CD的长是（ ）| A． | 2 | B． | 1 | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |