题目内容
14.已知,如图,点A、C、F、D在一条直线上,AF=DC,AB=DE,BC=EF.(1)求证:AB∥DE,BC∥EF;
(2)把图中的△DEF沿直线AD平移到四个不同的位置,仍能证明上面选择其中的一个图形进行证明;
(3)在△DEF平移的过程中.哪些量是变化的?哪些量是不变的?说明理由.

分析 (1)根据等式的性质,可得DF与AC的关系,根据SSS,可得△DEF与△ABC的关系,根据全等三角形的性质,可得∠DFE与∠ACB的关系,根据平行线的判定,可得答案;
(2)如图③,根据已知条件得到△DEF≌△ABC,根据全等三角形的性质得到∠BAC=∠FED,∠ACB=∠CFE,由平行线的判定定理即可得到AB∥DE,BC∥EF;
(3)根据平移的性质即可得到结论.
解答 (1)证明:∵CD=AF,
∴CD+CF=AF+CF,
即DF=AC.
在△DEF和△ABC中,
$\left\{\begin{array}{l}{DE=AB}\\{EF=BC}\\{DF=AC}\end{array}\right.$,
∴△DEF≌△ABC,
∴∠A=∠D,∠ACB=∠CFE,
∴AB∥DE,∠DFE=∠ACB,
∴BC∥EF;
(2)如图③,
在△DEF和△ABC中,
$\left\{\begin{array}{l}{DE=AB}\\{EF=BC}\\{DF=AC}\end{array}\right.$,
∴△DEF≌△ABC,
∴∠BAC=∠FED,∠ACB=∠CFE,
∴AB∥DE,BC∥EF;
(3)在△DEF平移的过程中,线段AF,CD是变化的,AB,BC,AC,DF,EF,DE是不变的,
理由:在△DEF平移的过程中,△DEF的大小,形状不发生变化,位置发生变化.
点评 本题考查了全等三角形的判定和性质,平移的性质,熟记平移的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知-7是关于x的方程2x-7=ax的解,则a的值是( )
| A. | -2 | B. | -3 | C. | 3 | D. | -14 |
 如图,AB是⊙O的直径,C是⊙O上一点,且BC=3,AC=5,CP平分∠ACB交⊙O于点P,交直径AB于点D,则线段CP的长为4$\sqrt{2}$.
如图,AB是⊙O的直径,C是⊙O上一点,且BC=3,AC=5,CP平分∠ACB交⊙O于点P,交直径AB于点D,则线段CP的长为4$\sqrt{2}$. 如图,已知AC、BD相交于O,AE=FC,AO=OC,BO=OD.求证:∠1=∠2.
如图,已知AC、BD相交于O,AE=FC,AO=OC,BO=OD.求证:∠1=∠2. 如图,已知AB=AD,若AC平分∠BAD,AC是否平分∠BCD?为什么?
如图,已知AB=AD,若AC平分∠BAD,AC是否平分∠BCD?为什么?
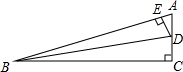 如图,在Rt△ABC中,∠C=90°,点D,E分别在边AC,AB上,BD是∠ABC的平分线,DE⊥AB,AE=10,cosA=$\frac{5}{13}$.
如图,在Rt△ABC中,∠C=90°,点D,E分别在边AC,AB上,BD是∠ABC的平分线,DE⊥AB,AE=10,cosA=$\frac{5}{13}$.