题目内容
6.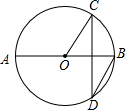 如图,AB是⊙O的直径,AB=4,弦CD⊥AB,∠CDB=30°,则CD的长是( )
如图,AB是⊙O的直径,AB=4,弦CD⊥AB,∠CDB=30°,则CD的长是( )| A. | 2 | B. | 1 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 由圆周角定理得出∠BOC=2∠CDB=60°,由垂径定理得出CD=2CE,∠C=30°,求出OE=$\frac{1}{2}$OC=1,由勾股定理得出CE,即可得出CD的长.
解答 解:如图所示:
∵AB是⊙O的直径,AB=4,
∴OC=OA=2,
∵∠BOC=2∠CDB=60°,
∵CD⊥AB,
∴CD=2CE,∠C=90°-60°=30°,
∴OE=$\frac{1}{2}$OC=1,
∴CE=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴CD=2CE=2$\sqrt{3}$;
故选:D.
点评 本题考查了垂径定理、圆周角定理、勾股定理、含30°角的直角三角形的性质;熟练掌握垂径定理,由勾股定理求出CE是解决问题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
18. 如图,一条抛物线与x轴相交于A、B两点,其顶点E在线段CD上移动,若点C、D的坐标分别为(-1,4)、(4,4),点B的横坐标的最大值为6,则点A的横坐标的最小值为( )
如图,一条抛物线与x轴相交于A、B两点,其顶点E在线段CD上移动,若点C、D的坐标分别为(-1,4)、(4,4),点B的横坐标的最大值为6,则点A的横坐标的最小值为( )
 如图,一条抛物线与x轴相交于A、B两点,其顶点E在线段CD上移动,若点C、D的坐标分别为(-1,4)、(4,4),点B的横坐标的最大值为6,则点A的横坐标的最小值为( )
如图,一条抛物线与x轴相交于A、B两点,其顶点E在线段CD上移动,若点C、D的坐标分别为(-1,4)、(4,4),点B的横坐标的最大值为6,则点A的横坐标的最小值为( )| A. | 2 | B. | 0 | C. | -2 | D. | -3 |
13.如图是2012年10月份的日历,用一正方形在表中随意框住4个数.
(1)如果把其中最小的数记为x,另外三个数用含x的式子表示出来,则从小到大依次是x+1,x+7,x+8.
(2)当这4个数之和等于100时,求x的值并在图中框住这四个数.
(3)被框住的四个数之和能否等于136?如果能,请求出此时x的值;如果不能,请说明理由.
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
(2)当这4个数之和等于100时,求x的值并在图中框住这四个数.
(3)被框住的四个数之和能否等于136?如果能,请求出此时x的值;如果不能,请说明理由.
 如图,已知AB=AD,若AC平分∠BAD,AC是否平分∠BCD?为什么?
如图,已知AB=AD,若AC平分∠BAD,AC是否平分∠BCD?为什么?
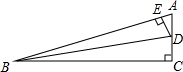 如图,在Rt△ABC中,∠C=90°,点D,E分别在边AC,AB上,BD是∠ABC的平分线,DE⊥AB,AE=10,cosA=$\frac{5}{13}$.
如图,在Rt△ABC中,∠C=90°,点D,E分别在边AC,AB上,BD是∠ABC的平分线,DE⊥AB,AE=10,cosA=$\frac{5}{13}$.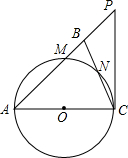 如图,在△ABC中,AB=AC,以AC为直径的⊙O分别交AB,BC于点M,N,过点C作⊙O的切线交AB的延长线于点P.
如图,在△ABC中,AB=AC,以AC为直径的⊙O分别交AB,BC于点M,N,过点C作⊙O的切线交AB的延长线于点P.