题目内容
12.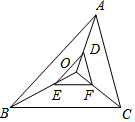 如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )
如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
分析 根据已知条件得到EF∥BC,推出△EOF∽△BOC,根据相似三角形的性质即可得到结论.
解答 解:∵$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,
∴EF∥BC,
∴△EOF∽△BOC,
∴$\frac{EF}{BC}$=$\frac{OF}{OC}$,
∵$\frac{OF}{CF}$=$\frac{1}{2}$,
∴$\frac{OF}{OC}$=$\frac{1}{3}$,
∴$\frac{EF}{BC}$=$\frac{1}{3}$,
故选B.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
20.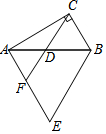 如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )
如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )
 如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )
如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{3}{2}$ |
7.已知sinA=$\frac{1}{2}$,则∠A的度数为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
17.在 Rt△ABC中,∠C=90°,∠A-∠B=70°,则∠A的度数为( )
| A. | 80° | B. | 70° | C. | 60° | D. | 50° |
2.下列计算正确的是( )
| A. | 6-(-6)=0 | B. | (-2.8)+1.2=1.6 | C. | (+2)+(-5)=-3 | D. | $\frac{1}{3}-({-\frac{2}{3}})=-\frac{1}{3}$ |