题目内容
12.为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:| 污水处理设备 | A型 | B型 |
| 价格(万元/台) | m | m-3 |
| 月处理污水量(吨/台) | 2200 | 1800 |
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问采用何种购买方案可以使得每月处理污水量的吨数为最多?并求出最多吨数.
分析 (1)根据90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,列出关于m的分式方程,求出m的值即可;
(2)设购买A型设备x台,则B型设备(10-x)台,根据题意列出关于x的一元一次不等式,求出x的取值范围.再设每月处理污水量为W吨,则W=2200x+1800(10-x)=400x+18000,根据一次函数的性质即可求出最大值.
解答 解:(1)由题意得:$\frac{90}{m}$=$\frac{75}{m-3}$,
解得m=18.
经检验m=18是原方程的根,
故m的值为18;
(2)设购买A型设备x台,则B型设备(10-x)台,
由题意得:18x+15(10-x)≤165,
解得x≤5.
设每月处理污水量为W吨,由题意得W=2200x+1800(10-x)=400x+18000,
∵400>0,
∴W随着x的增大而增大,
∴当x=5时,W最大值为:400×5+18000=20000,
即两种设备各购入5台,可以使得每月处理污水量的吨数为最多,最多为20000吨.
点评 本题考查分式方程的应用,一次函数的应用和一元一次不等式的应用,分析题意,找到合适的关系是解决问题的关键.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.

练习册系列答案
相关题目
20.二元一次方程组$\left\{\begin{array}{l}x+y=1\\ x-y=3\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
7.某校人数相等的甲、乙两个班同时进行测验,班级的平均分和方差分别为:$\overline{{x}_{甲}}$=78分,$\overline{{x}_{乙}}$=78分,s甲2=180,s乙2=80,那么成绩较为整齐的是( )
| A. | 甲班 | B. | 两个班一样整齐 | C. | 乙班 | D. | 无法确定 |
1.若a>b,则下列不等式变形正确的是( )
| A. | a+5<b+5 | B. | $\frac{a}{3}>\frac{b}{3}$ | C. | -4a>-4b | D. | 3a-2<3b-2 |
2.若a<b,则下列不等式中正确的是( )
| A. | 2a>2b | B. | a-b>0 | C. | -3a>-3b | D. | a-3<b-5 |
 如图,在?ABCD中,∠ABC的平分线交AD于点E,AB=4,BC=6,则DE的长为2.
如图,在?ABCD中,∠ABC的平分线交AD于点E,AB=4,BC=6,则DE的长为2.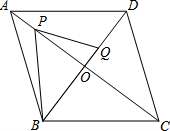 如图,已知菱形ABCD,对角线AC、BD相交于点O,AB=10,AC=16.点P在AO上,点Q在DO上,且AP=2OQ.
如图,已知菱形ABCD,对角线AC、BD相交于点O,AB=10,AC=16.点P在AO上,点Q在DO上,且AP=2OQ.