题目内容
3.已知:如图,AB∥CD.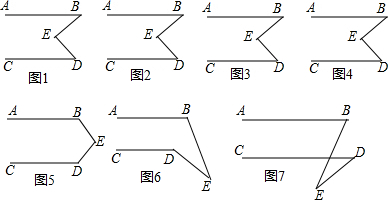
(1)如图1,猜想并写出∠B、∠D、∠E之间的数量关系,图2、图3、图4是三种不同角度思考采用的不同添加辅助线的方式,请你选择其中的两种方式说明理由.
(2)在图4中,如果BE、DE分别平分∠ABD、∠CDB,则∠E的度数是多少?(直接写出答案)
(3)根据以上推理,直接写出图5、图6、图7中的∠B、∠D、∠E之间的数量关系.
分析 (1)①过E作EF∥AB,根据平行线的性质推出即可;②连接BD,根据平行线的性质推出即可;③延长BE交CD于Q,根据平行线的性质和三角形外角性质得出即可;
(2)根据平行线的性质得出∠ABD+∠CDB=180°,求出∠EBD+∠EDB=90°,根据三角形外角性质得出即可;
(3)根据平行线的性质和图形得出即可.
解答 解:(1)∠B+∠D=∠E,
理由是:如图1: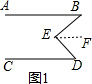
过E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠BEF,∠D=∠DEF,
∴∠B+∠D=∠BEF+∠DEF=∠BED;
∠B+∠D=∠E,
理由是:如图2,连接BD,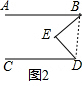
∵AB∥CD,
∴∠ABD+○EBD+∠CDE+∠BDE=180°,
∵∠BED+∠EBD+∠BDE=180°,
∴∠ABE+∠CDE=∠BED;
∠B+∠D=∠E,
理由是:如图3,延长BE交CD于Q,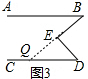
∵AB∥CD,
∴∠B=∠BQD,
∵∠BQD+∠D=∠BED,
∴∠B+∠D=∠BED;
(2)∠BED=90°,
理由是:如图4: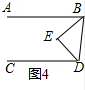
∵AB∥CD,
∴∠ABD+∠CDB=180°,
∵BE、DE分别平分∠ABD、∠CDB,
∴∠EBD=$\frac{1}{2}$∠ABD,∠BDE=$\frac{1}{2}$∠CDB,
∴∠EBD+∠DBE=90°,
∴∠BED=180°-90°=90°;
(3)图5中∠B+∠E+∠D=360°;图6中∠B+∠E=∠D;图7中∠B+∠D+∠E=180°.
点评 本题考查了平行线的性质,三角形的外角性质,三角形内角和定理的应用,能正确作出辅助线是解此题的关键,难度适中.

练习册系列答案
相关题目
8.2014年全年国内生产总值按可比价格计算,比上年增长9.5%,达到136500亿元.136500亿元用科学记数法表示为( )
| A. | 1.365×1012元 | B. | 13.65×1012元 | C. | 1.365×1013元 | D. | 0.1365×1014元 |
12.为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问采用何种购买方案可以使得每月处理污水量的吨数为最多?并求出最多吨数.
| 污水处理设备 | A型 | B型 |
| 价格(万元/台) | m | m-3 |
| 月处理污水量(吨/台) | 2200 | 1800 |
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问采用何种购买方案可以使得每月处理污水量的吨数为最多?并求出最多吨数.
13.方程x(x-3)=(x-3)的解是( )
| A. | 1 | B. | 3 | C. | 1或3 | D. | 0 |
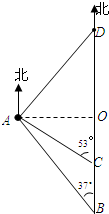 如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.
如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.