题目内容
1.若a>b,则下列不等式变形正确的是( )| A. | a+5<b+5 | B. | $\frac{a}{3}>\frac{b}{3}$ | C. | -4a>-4b | D. | 3a-2<3b-2 |
分析 利用不等式的基本性质变形得到结果,即可做出判断.
解答 解:由a>b,变形得:$\frac{a}{3}$>$\frac{b}{3}$,
故选B
点评 此题考查了不等式的性质,熟练掌握不等式的基本性质是解本题的关键.

练习册系列答案
相关题目
12.为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问采用何种购买方案可以使得每月处理污水量的吨数为最多?并求出最多吨数.
| 污水处理设备 | A型 | B型 |
| 价格(万元/台) | m | m-3 |
| 月处理污水量(吨/台) | 2200 | 1800 |
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问采用何种购买方案可以使得每月处理污水量的吨数为最多?并求出最多吨数.
13.方程x(x-3)=(x-3)的解是( )
| A. | 1 | B. | 3 | C. | 1或3 | D. | 0 |
10. 如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:
如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:
①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④∠BDC=$\frac{1}{2}$∠BAC.其中正确的结论有( )
 如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:
如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④∠BDC=$\frac{1}{2}$∠BAC.其中正确的结论有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
11. 如图,在?ABCD中,E、F是对角线AC上的两点,且AE=CF,在:
如图,在?ABCD中,E、F是对角线AC上的两点,且AE=CF,在:
①△ADE≌△CBF;②BE=DE;③BE∥DF;④∠EBF=∠EDF;⑤S△EBC=S△ADF.
这些结论中正确的有( )
 如图,在?ABCD中,E、F是对角线AC上的两点,且AE=CF,在:
如图,在?ABCD中,E、F是对角线AC上的两点,且AE=CF,在:①△ADE≌△CBF;②BE=DE;③BE∥DF;④∠EBF=∠EDF;⑤S△EBC=S△ADF.
这些结论中正确的有( )
| A. | ①②③④⑤ | B. | ①②③⑤ | C. | ①②③④ | D. | ①③④⑤ |
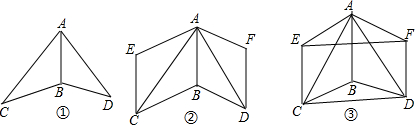
 如图,已知AB∥CD,AE∥CF,量一量、猜一猜∠BAE与∠DCF有什么数量关系,说明理由.
如图,已知AB∥CD,AE∥CF,量一量、猜一猜∠BAE与∠DCF有什么数量关系,说明理由.