题目内容
18.阅读下列材料:(1)关于x的方程x2-3x+1=0(x≠0)方程两边同时乘以$\frac{1}{x}$得:$x-3+\frac{1}{x}=0$即$x+\frac{1}{x}=3$,${({x+\frac{1}{x}})^2}={x^2}+\frac{1}{x^2}+2•x•\frac{1}{x}={x^2}+\frac{1}{x^2}+2$,${x^2}+\frac{1}{x^2}={({x+\frac{1}{x}})^2}-2={3^2}-2=7$
(2)a3+b3=(a+b)(a2-ab+b2);a3-b3=(a-b)(a2+ab+b2).
根据以上材料,解答下列问题:
(1)x2-4x+1=0(x≠0),则$x+\frac{1}{x}$=4,${x^2}+\frac{1}{x^2}$=14,${x^4}+\frac{1}{x^4}$=194;
(2)2x2-7x+2=0(x≠0),求${x^3}+\frac{1}{x^3}$的值.
分析 (1)模仿例题利用完全平方公式即可解决.
(2)模仿例题利用完全平方公式以及立方和公式即可.
解答 解;(1)∵x2-4x+1=0,
∴x+$\frac{1}{x}$=4,
∴(x+$\frac{1}{x}$)2=16,
∴x2+2+$\frac{1}{{x}^{2}}$=16,
∴x2+$\frac{1}{{x}^{2}}$=14,
∴(x2+$\frac{1}{{x}^{2}}$)2=196,
∴x4+$\frac{1}{{x}^{4}}$+2=196,
∴x4+$\frac{1}{{x}^{4}}$=194.
故答案为4,14,194.
(2)∵2x2-7x+2=0,
∴x+$\frac{1}{x}$=$\frac{7}{2}$,x2+$\frac{1}{{x}^{2}}$=$\frac{41}{4}$,
∴${x^3}+\frac{1}{x^3}$=(x+$\frac{1}{x}$)(x2-1+$\frac{1}{{x}^{2}}$)=$\frac{7}{2}$×($\frac{41}{4}$-1)=$\frac{259}{8}$.
点评 本题考查一元一次方程的解、完全平方公式、立方和公式,解决问题的关键是灵活应用完全平方公式,记住两边平方不能漏项(利用完全平方公式整体平方),属于中考常考题型.

练习册系列答案
相关题目
13.已知关于x的方程x2-3mx+5m-2=0的一个根为x=2,且这个方程的两个根恰好是等腰△ABC的两条边长,则△ABC的周长为( )
| A. | 8 | B. | 10 | C. | 8或10 | D. | 6或10 |
7.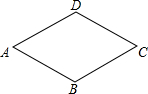 如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )
如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )
 如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )
如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )| A. | 16 | B. | 16$\sqrt{2}$ | C. | 16$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
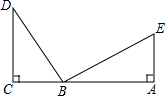 如图,DC⊥CA,EA⊥CA,CD=AB,CB=AE.求证:∠D=∠EBA.
如图,DC⊥CA,EA⊥CA,CD=AB,CB=AE.求证:∠D=∠EBA. 如图,若∠1=35°,则∠2=145°,∠3=35°.
如图,若∠1=35°,则∠2=145°,∠3=35°.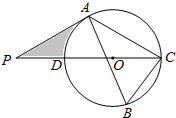 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.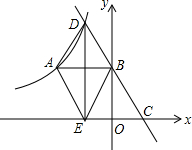 如图所示,在平面直角坐标系中,双曲线y=$\frac{k}{x}$(x<0)上有一点A(-2,2),AB⊥y轴于点B,点C是x轴正半轴上一动点,直线CB交双曲线于点D,DE⊥x轴于点E,连接AE,AD,BE.
如图所示,在平面直角坐标系中,双曲线y=$\frac{k}{x}$(x<0)上有一点A(-2,2),AB⊥y轴于点B,点C是x轴正半轴上一动点,直线CB交双曲线于点D,DE⊥x轴于点E,连接AE,AD,BE.