题目内容
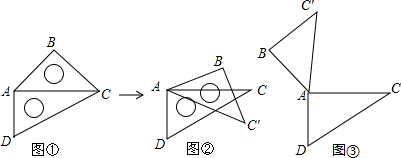
8.取一副三角板按图①拼接,固定三角板ADC(∠ACD=30°),将三角板ABC(∠ACB=45°)绕点A依顺时针方向旋转一定的角度得到△ABC′,请问:(1)如图②,当∠CAC′=15°时,请你判断AB与CD的位置关系,并说明理由;
(2)如图③,当∠CAC′为多少度时,能使CD∥BC′?(直接回答,不用证明)
分析 (1)求出∠BAC=30°,得出∠BAC=∠C=30°,即可证出AB∥CD;
(2)如答图2,连接C′D.在△AC′D中利用三角形内角和定理进行解答即可.
解答 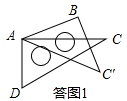 解:(1)如答图1,∵∠BAC=∠BAC′-∠CAC′=45°-15°=30°,
解:(1)如答图1,∵∠BAC=∠BAC′-∠CAC′=45°-15°=30°,
∴∠BAC=∠C=30°,
∴AB∥CD;
(2)当∠CAC′=755°时,能使CD∥BC′,理由如下,
如答图③,延长BA交CD于点E.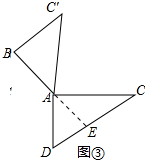
∵CD∥BC′,
∴∠B+∠AEC=180°,∵∠B=90°,
∴∠AEC=90°,∵∠C=30°
∴∠CAE=60°
∴∠C′AC=180°-(∠CAE+∠BAC′)=180°-105°=75°.
点评 本题考查了平行线的判定与性质、三角形内角和定理;熟练掌握平行线的判定和三角形内角和定理,并能进行推理计算是解决问题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
19.下列计算正确的是( )
| A. | $\root{3}{8}=±2$ | B. | -$\root{3}{-7}=-\root{3}{7}$ | C. | $-\sqrt{\frac{16}{9}}=-\frac{4}{3}$ | D. | $\sqrt{\frac{9}{4}}=±\frac{3}{2}$ |
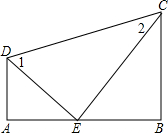 已知:如图,DA⊥AB,DE平分∠ADC,CE平分∠BCD,且∠DEC=90°.试猜想BC与AB有怎样的位置关系,并说明其理由.
已知:如图,DA⊥AB,DE平分∠ADC,CE平分∠BCD,且∠DEC=90°.试猜想BC与AB有怎样的位置关系,并说明其理由.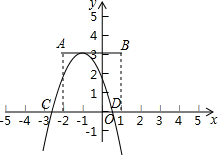 已知点A,B的坐标分别为(-2,3)和(1,3),平移抛物线y=ax2+bx+c(a<0),该抛物线的顶点在线段AB上运动,与x轴交于C、D两点.
已知点A,B的坐标分别为(-2,3)和(1,3),平移抛物线y=ax2+bx+c(a<0),该抛物线的顶点在线段AB上运动,与x轴交于C、D两点.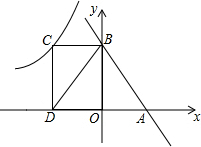 如图,直线y=-x+2与x轴、y轴分别交于A、B两点,过B点作BC⊥y轴与双曲线y=$\frac{k}{x}$(k<0)交于C点,过C作CD⊥x轴于D.若△BOD的面积为3,则k的值为-6.
如图,直线y=-x+2与x轴、y轴分别交于A、B两点,过B点作BC⊥y轴与双曲线y=$\frac{k}{x}$(k<0)交于C点,过C作CD⊥x轴于D.若△BOD的面积为3,则k的值为-6. 如图,在四边形ABCD中,AB∥CD,AD=BC,对角线AC⊥BD,AB=2,CD=6,则四边形ABCD的面积为24.
如图,在四边形ABCD中,AB∥CD,AD=BC,对角线AC⊥BD,AB=2,CD=6,则四边形ABCD的面积为24.