题目内容
16.已知a1、a2、a3、a4是彼此不相等的负数,且M=(a1+a2+a3)(a2+a3+a4),N=(a1+a2+a3+a4)(a2+a3),那么M与N的大小关系是M>N.(填“>”,“<”或“=”)分析 代入求出M-N,根据多项式乘以多项式法则展开,再合并同类项,根据求出的结果得出M-N>0,即可求出答案.
解答 解:∵M=(a1+a2+a3)(a2+a3+a4),N=(a1+a2+a3+a4)(a2+a3),
∴M-N=(a1+a2+a3)(a2+a3+a4)-(a1+a2+a3+a4)(a2+a3)
=(a1+a2+a3)(a2+a3)+(a1+a2+a3)•a4-(a1+a2+a3)(a2+a3)-a4(a2+a3)
=(a1+a2+a3)•a4-a4(a2+a3)
=a1•a4>0,
∴M-N>0,
∴M>N,
故答案为:>.
点评 本题考查了整式的混合运算,能选择适当的方法比较两个数的大小是解此题的关键,注意:用了整体代入思想.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
8.“元旦”期间,某文具店购进100只两种型号的文具进行销售,其进价和售价如下表:
(1)该店用1300元可以购进A,B两种型号的文具各多少只?
(2)若把所购进A,B两种型号的文具全部销售完,利润率超过40%没有?请你说明理由.
| 型号 | 进价(元/只) | 售价(元/只) |
| A型 | 10 | 12 |
| B型 | 15 | 23 |
(2)若把所购进A,B两种型号的文具全部销售完,利润率超过40%没有?请你说明理由.
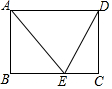 如图,矩形ABCD中,AE平分∠BAD,并交BC于点E,ED=5cm,EC=3cm,则矩形的周长为22cm,面积为28cm2.
如图,矩形ABCD中,AE平分∠BAD,并交BC于点E,ED=5cm,EC=3cm,则矩形的周长为22cm,面积为28cm2.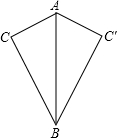 如图所示,∠C=∠C′=90°,AC=AC′,求证:∠CAB=∠C′AB(要求不用全等的知识证明).
如图所示,∠C=∠C′=90°,AC=AC′,求证:∠CAB=∠C′AB(要求不用全等的知识证明). 如图,AD平分∠BAC,其中∠B=35°,∠ADC=82°,求∠BAC,∠C的度数.
如图,AD平分∠BAC,其中∠B=35°,∠ADC=82°,求∠BAC,∠C的度数.