题目内容
1. 如图,AD平分∠BAC,其中∠B=35°,∠ADC=82°,求∠BAC,∠C的度数.
如图,AD平分∠BAC,其中∠B=35°,∠ADC=82°,求∠BAC,∠C的度数.
分析 首先根据邻补角的知识求出∠ADB的度数,再根据三角形内角和定理求出∠BAD的度数,又根据角平分线的知识求出∠BAC的度数,最后再次利用三角形内角和定理求出∠C的度数.
解答 解:∵∠ADC=82°,
∴∠ADB=180°-82°=98°,
∴∠BAD=180°-∠B-∠ADB=180°-35°-98°=46°,
∵AD平分∠BAC,
∴∠BAC=2∠BAD=2×46°=92°,
∴∠C=180°-35°-92°=53°.
点评 本题主要考查了三角形内角和定理的知识,解题的关键是掌握三角形的内角和为180°,此题难度不大.

练习册系列答案
相关题目
6.要调查某校学生周日的睡眠时间,下列调查对象选取最合适的是( )
| A. | 选取该校50名女生 | B. | 选取该校50名男生 | ||
| C. | 选取该校一个班级的学生 | D. | 随机选取该校50名学生 |
13.顶点是(2,-1)的抛物线的表达式是( )
| A. | y=-(x-2)2-1 | B. | y=(x+2)2-1 | C. | y=3(x-2)2+1 | D. | y=2(x-1)2+1 |
10.将代数式x2-2x+2化为(x+p)2+q的形式,正确的是( )
| A. | (x-1)2-3 | B. | (x-1)2+1 | C. | (x+1)2+2 | D. | (x+1)2+1 |

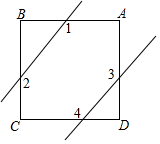 如图,正方形ABCD中,截去∠B、∠D后,∠1、∠2、∠3、∠4的和为540°.
如图,正方形ABCD中,截去∠B、∠D后,∠1、∠2、∠3、∠4的和为540°.