Question

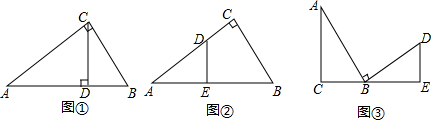
14．（1）如图①，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，∠ACD与∠B有什么关系？为什么？
（2）如图②，在Rt△ABC中，∠C=90°，D、E分别在AC，AB上，且∠ADE=∠B，判断△ADE的形状是什么？为什么？
（3）如图③，在Rt△ABC和Rt△DBE中，∠C=90°，∠E=90°，AB⊥BD，点C，B，E在同一直线上，∠A与∠D有什么关系？为什么？

Answer 1

分析 （1）根据直角三角形的性质得出∠ACD+∠A=∠B+∠DCB=90°，再解答即可；
（2）根据直角三角形的性质得出∠ADE+∠A=∠A+∠B=90°，再解答即可；
（3）根据直角三角形的性质得出∠ABC+∠A=∠ABC+∠DBE=∠DBE+∠D=90°，再解答即可．

解答 解：（1）∠ACD=∠B，理由如下：
∵在Rt△ABC中，∠ACB=90°，CD⊥AB，
∴∠ACD+∠A=∠B+∠DCB=90°，
∴∠ACD=∠B；

（2）△ADE是直角三角形．
∵在Rt△ABC中，∠C=90°，D、E分别在AC，AB上，且∠ADE=∠B，∠A为公共角，
∴∠AED=∠ACB=90°，
∴△ADE是直角三角新；

（3）∠A+∠D=90°．
∵在Rt△ABC和Rt△DBE中，∠C=90°，∠E=90°，AB⊥BD，
∴∠ABC+∠A=∠ABC+∠DBE=∠DBE+∠D=90°，
∴∠A+∠D=90°．

点评 此题考查直角三角形的性质，关键是根据直角三角形的性质得出两锐角互余．