题目内容
2．M、N分别为△ABC的边AB，AC的中点，则△ADE与梯形DBCE的面积比为1：3．分析 由题意可知△AMN∽△ABC且相似比是1：2，根据相似比求面积比．
解答 解：∵M，N分别是AB，AC的中点，
∴MN∥BC，
∴△AMN∽△ABC，
∴AM：AB=1：2，
∴△AMN与△ABC的面积之比为1：4，
∴△AMN与四边形MBCN的面积之比是1：3．
故答案为：1：3．
点评 本题考查对相似三角形性质的理解，相似三角形面积的比等于相似比的平方．
练习册系列答案
相关题目
12．
如图所示，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作正△ABC和正△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下四个结论：①△ACD≌△BCE；②AD=BE；③∠AOB=60°；④△CPQ是等边三角形．
其中正确的是（ ）
如图所示，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作正△ABC和正△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下四个结论：①△ACD≌△BCE；②AD=BE；③∠AOB=60°；④△CPQ是等边三角形．其中正确的是（ ）
| A． | ①②③④ | B． | ②③④ | C． | ①③④ | D． | ①②③ |
13．
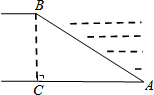河堤的横断面如图所示，迎水坡AB=10米，迎水坡AB的坡比$1：\sqrt{3}$（坡比是坡面的垂直高度与水平宽度之比），则AC的长是（ ）
河堤的横断面如图所示，迎水坡AB=10米，迎水坡AB的坡比$1：\sqrt{3}$（坡比是坡面的垂直高度与水平宽度之比），则AC的长是（ ）| A． | 5米 | B． | $5\sqrt{3}$米 | C． | $\frac{{5\sqrt{3}}}{3}$米 | D． | $\frac{{10\sqrt{3}}}{3}$米 |
10．二次函数y=2x2-3x-1的二次项系数与常数项的和是（ ）
| A． | 1 | B． | -1 | C． | 5 | D． | -4 |
已知△ABC和点O，画出△DEF，使△DEF与△ABC关于O成中心对称．
如图：△ABC中，AB=2，AC=1，以AB为直径的圆与AC相切，与边BC交于点D．求出线段AD的长．