题目内容
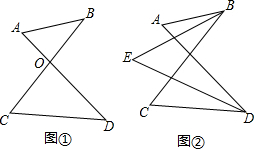
5.“8字”的性质及应用:(1)如图①,AD、BC相交于点O,得到一个“8字”ABCD,求证:∠A+∠B=∠C+∠D.
(2)图②中共有多少个“8字”?
(3)如图②,∠ABC和∠ADC的平分线相交于点E,利用(1)中的结论证明∠E=$\frac{1}{2}$(∠A+∠C).
分析 (1)根据三角形内角和定理和对顶角相等解答即可;
(2)根据题中给出的“8字”的概念解答即可;
(3)根据角平分线的定义和三角形的外角的性质解答即可.
解答 解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,又∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)图②中有:ABCD、BECD、ABED,3个“8字”;
(3)∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠CBE=$\frac{1}{2}∠$ABC,∠CDE=∠ADE=$\frac{1}{2}$∠ADC,
∵∠A+∠ABE=∠E+∠ADE,∠C+∠CDE=∠E+∠CBE,
∴∠E=$\frac{1}{2}$(∠A+∠C).
点评 本题考查的是三角形内角和定理、三角形外角的性质和对顶角相等的综合运用,掌握三角形内角和等于180°和三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.

练习册系列答案
相关题目
17.下列说法中错误的是( )
| A. | 数轴上的点与实数一一对应 | B. | 实数中没有最小的数 | ||
| C. | a、b为实数,若a<b,则$\sqrt{a}$<$\sqrt{b}$ | D. | a、b为实数,若a<b,则$\root{3}{a}$<$\root{3}{b}$ |
 如图,以点B为顶点,射线BC为一边,利用尺规作∠EBC,使得∠EBC=∠A.
如图,以点B为顶点,射线BC为一边,利用尺规作∠EBC,使得∠EBC=∠A.


