题目内容
20.已知在边长为2的正方形ABCD中,E为AD中点,连接BE,以E为圆心,EB为半径画弧交DA的延长线于F,再以AF为边作正方形AFGH,判断H是否为AB的黄金分割点,并说明理由.分析 根据题意求出AF的长,即求出AH的长,从而求出AH与AB的比值,根据黄金比值得到答案.
解答  解:如图,∵AD=2,E为AD中点,
解:如图,∵AD=2,E为AD中点,
∴AE=1,
在Rt△AEB中,由勾股定理得BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{5}$,
由于BE=EF,则AF=BE-AE=$\sqrt{5}$-1,
∵AH=AF=$\sqrt{5}$-1,
∴AH:AB=$\frac{\sqrt{5}-1}{2}$,
∴H为AB的黄金分割点.
点评 本题考查的是黄金分割点的知识和正方形的性质,掌握$\frac{\sqrt{5}-1}{2}$叫做黄金比是解题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
10.下列各式中是二元一次方程的是( )
| A. | x+3y=5 | B. | -xy-y=1 | C. | 2x-y+1 | D. | $\frac{x}{2}$+$\frac{7}{y}$=$\frac{1}{5}$ |
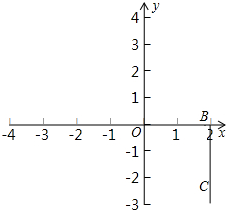 如图,长方形ABCD三个顶点的坐标分别是A(0,0),B(2,0),C(2,-2).
如图,长方形ABCD三个顶点的坐标分别是A(0,0),B(2,0),C(2,-2).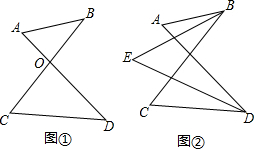
 如图,AB∥CD,AD∥BC,点E、A、B在同一直线上,AD平分∠EAC,AC平分∠BAD,
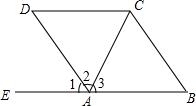
如图,AB∥CD,AD∥BC,点E、A、B在同一直线上,AD平分∠EAC,AC平分∠BAD,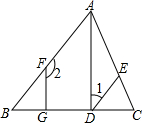 已知,如图∠B=∠EDC,∠1+∠2=180°,FG⊥BC,求证:AD⊥BC.
已知,如图∠B=∠EDC,∠1+∠2=180°,FG⊥BC,求证:AD⊥BC.