题目内容
12.在平面直角坐标系中,△ABC顶点A的坐标为(2,3),若以原点O为位似中心,画△ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比等于2:1,则点A′的坐标(1,$\frac{3}{2}$),(-1,-$\frac{3}{2}$).分析 根据在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k,即可求得答案.
解答 解:在同一象限内,∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,3),
∴则点A′的坐标为:(1,$\frac{3}{2}$),
不在同一象限内,∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,3),
∴则点A′的坐标为:(-1,-$\frac{3}{2}$),
故答案为:(1,$\frac{3}{2}$),(-1,-$\frac{3}{2}$).
点评 此题考查了位似图形的性质,此题比较简单,注意在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
2.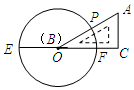 如图,已知EF是圆O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与圆O交于点P,点B与点O重合;将三角形ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x°,则x的取值范围是( )
如图,已知EF是圆O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与圆O交于点P,点B与点O重合;将三角形ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x°,则x的取值范围是( )
 如图,已知EF是圆O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与圆O交于点P,点B与点O重合;将三角形ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x°,则x的取值范围是( )
如图,已知EF是圆O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与圆O交于点P,点B与点O重合;将三角形ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x°,则x的取值范围是( )| A. | 60≤x≤120 | B. | 30≤x≤60 | C. | 30≤x≤90 | D. | 30≤x≤120 |
20.在等边△ABC内部任取一点P,将△ABP绕点A旋转到△ACQ,则△APQ为( )
| A. | 不等腰的直角三角形 | B. | 腰和底不等的等腰三角形 | ||
| C. | 等腰直角三角形 | D. | 等边三角形 |
7.将抛物线y=x2-2向左平移1个单位后再向上平移1个单位所得抛物线的表达式为( )
| A. | y=(x-1)2-1 | B. | y=(x+1)2-1 | C. | y=(x+1)2+1 | D. | y=(x-1)2+1 |
17.计算:$\sqrt{8}$-$\sqrt{2}$,正确的是( )
| A. | 4 | B. | $\sqrt{6}$ | C. | 2 | D. | $\sqrt{2}$ |
4.洪峰到来前,120名战士奉命加固堤坝,已知5人运沙袋3人堆垒沙袋,正好运来的沙袋能及时用上且不窝工,为了合理安排,如果设x人运送沙袋,其余人堆垒沙袋,那么以下所列方程正确的是( )
| A. | $\frac{120-x}{2}$=x | B. | 120-x=$\frac{5}{3}$x | C. | x=$\frac{5}{3}$(120-x) | D. | 3x+2x=120 |
