题目内容
2.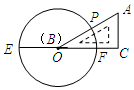 如图,已知EF是圆O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与圆O交于点P,点B与点O重合;将三角形ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x°,则x的取值范围是( )
如图,已知EF是圆O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与圆O交于点P,点B与点O重合;将三角形ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x°,则x的取值范围是( )| A. | 60≤x≤120 | B. | 30≤x≤60 | C. | 30≤x≤90 | D. | 30≤x≤120 |
分析 根据直角三角形两锐角互余求出∠ABC=30°,从而得到点B与点O重合时∠POF=30°,再根据在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半求出点B与点E重合时∠POF=2∠ABC,然后写出x的取值范围即可.
解答 解:∵∠A=60°,
∴∠ABC=30°,
①点B与点O重合时,∠POF=∠ABC=30°,
②点B与点E重合时,∠POF=2∠ABC=2×30°=60°,
所以,x的取值范围是30≤x≤60.
故选B.
点评 本题考查了圆周角定理,直角三角形两锐角互余,在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
7.对于有理数a、b,定义运算:a⊕b=a×b-a-b+1,则计算3⊕4的结果是( )
| A. | -12 | B. | 6 | C. | -6 | D. | 12 |
 按要求作图 如图,在同一平面内有四个点A、B、C、D
按要求作图 如图,在同一平面内有四个点A、B、C、D 每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,将△ABC绕点A逆时针旋转90°后得到△A′C′.
每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,将△ABC绕点A逆时针旋转90°后得到△A′C′.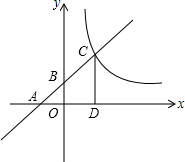 如图,已知一次函数y=kx+b(k≠0)的图象与x轴,y轴分别交于A,B两点,且与反此列函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于C点,CD⊥x轴于D.若OA=OB=OD=1,
如图,已知一次函数y=kx+b(k≠0)的图象与x轴,y轴分别交于A,B两点,且与反此列函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于C点,CD⊥x轴于D.若OA=OB=OD=1,