题目内容
15. 在△ABC中,
在△ABC中,(1)若∠A:∠B:∠C=1:2:3,则∠A=30°,∠B=60°,∠C=90°,此三角形为直角三角形;
(2)若∠A大于∠B+∠C,则此三角形为钝角三角形.
分析 (1)设∠A=x°,∠B=2x°,∠C=3x°,根据∠A+∠B+∠C=180°得出方程x+2x+3x=180,求出x即可;
(2)当∠A>∠B+∠C时,可得∠A>90°,可得到答案
解答 解:(1)∵∠A:∠B:∠C=1:2:3,
∴设∠A=x°,∠B=2x°,∠C=3x°,
∵∠A+∠B+∠C=180°,
∴x+2x+3x=180,
x=30,
∴∠A=30°,∠B=60°,∠C=90°,此三角形为直角三角形,
故答案为:30°,60°,90°,直角;
(2)当∠A>∠B+∠C时,可得∠A>90°,则△ABC为钝角三角形,
故答案为:钝角.
点评 本题主要考查三角形内角和定理,掌握三角形的三个内角和为180°是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
5.关于x的方程(m-2)x2+2x+1=0有实数根,则偶数m的最大值为( )
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
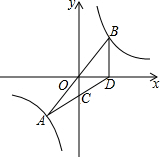 如图,A、B是反比例函数y=$\frac{k}{x}$(k>0)图象上关于原点O对称的两点,直线AC经过点C(0,-2)与x轴交于点D,若C为AD中点,△ABD的面积是5,则点B的坐标为($\frac{5}{4}$,4).
如图,A、B是反比例函数y=$\frac{k}{x}$(k>0)图象上关于原点O对称的两点,直线AC经过点C(0,-2)与x轴交于点D,若C为AD中点,△ABD的面积是5,则点B的坐标为($\frac{5}{4}$,4). 如图,△ABC中,AB=8,AC=6,BC=10,作BC的垂直平分线DE交AB于点D,则AD=$\frac{7}{4}$.
如图,△ABC中,AB=8,AC=6,BC=10,作BC的垂直平分线DE交AB于点D,则AD=$\frac{7}{4}$.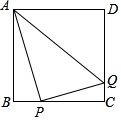 如图,正方形ABCD的边长为4,点P为BC边上的动点,连接AP,作PQ⊥AP,交CD于点Q,连接AQ,当点P从B点运动到C点时,线段AQ的中点所经过的路径长为1.
如图,正方形ABCD的边长为4,点P为BC边上的动点,连接AP,作PQ⊥AP,交CD于点Q,连接AQ,当点P从B点运动到C点时,线段AQ的中点所经过的路径长为1.


