题目内容
10. 如图,△ABC中,AB=8,AC=6,BC=10,作BC的垂直平分线DE交AB于点D,则AD=$\frac{7}{4}$.
如图,△ABC中,AB=8,AC=6,BC=10,作BC的垂直平分线DE交AB于点D,则AD=$\frac{7}{4}$.
分析 连接CD,首先利用勾股定理逆定理判定∠A=90°,再根据线段垂直平分线的性质可得DB=DC,设AD=x,则CD=8-x,再在Rt△ACD中利用勾股定理计算出AD长即可.
解答 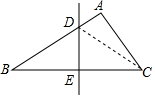 解:连接CD,
解:连接CD,
∵62+82=102,
∴AC2+AB2=BC2,
∴∠A=90°,
∵DE是BC的垂直平分线,
∴BD=CD,
∵AB=8,
∴AD+CD=8,
设AD=x,则CD=8-x,
在Rt△ACD中,AD2+AC2=CD2,
∴x2+62=(8-x)2,
解得:x=$\frac{7}{4}$,
∴AD=$\frac{7}{4}$,
故答案为:$\frac{7}{4}$.
点评 此题主要考查了勾股定理逆定理,以及线段垂直平分线的性质和勾股定理的应用,关键是正确判定∠A=90°,找出AD和CD之间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
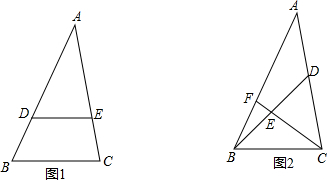
 ,则其代表的算式是(-65)2-5,结果是4220.
,则其代表的算式是(-65)2-5,结果是4220.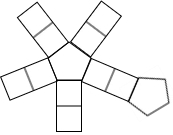 “磁力健构片”通过磁铁连接重心,可以轻松制作成球体、锥体、正方体等百种造型,立体提拉魔幻成型,直观立体,是全面开发脑力的益智玩具.如图所示的平面图形经过立体提拉后,会成型为( )
“磁力健构片”通过磁铁连接重心,可以轻松制作成球体、锥体、正方体等百种造型,立体提拉魔幻成型,直观立体,是全面开发脑力的益智玩具.如图所示的平面图形经过立体提拉后,会成型为( )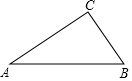 在△ABC中,
在△ABC中,


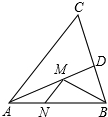 如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是3$\sqrt{2}$.
如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是3$\sqrt{2}$.