Question

20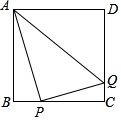．如图，正方形ABCD的边长为4，点P为BC边上的动点，连接AP，作PQ⊥AP，交CD于点Q，连接AQ，当点P从B点运动到C点时，线段AQ的中点所经过的路径长为1．

Answer 1

分析 由题意知：PQ⊥AP，即：∠APB+∠QPC=90°，∠BAP+∠APB=180°-∠B=90°，所以∠QPC=∠BAP，又∠B=∠C，即：△ABP∽△PCQ，由相似三角形的性质可得：$\frac{BP}{CQ}$=$\frac{AB}{PC}$，CQ=$\frac{PC}{AB}$×BP，又BP=x，PC=BC-BP=4-x，AB=4，将其代入该式求出CQ的值即可，利用“配方法”求该函数的最大值．易知点O的运动轨迹是O′→O→O′，CQ最大时，OO′=$\frac{1}{2}$CQ=$\frac{1}{2}$．

解答 解：如图，连接AC，设AC的中点为O′，AQ的中点为O．设BP的长为xcm，CQ的长为ycm．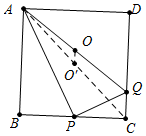

∵四边形ABCD是正方形，
∴∠B=∠C=90°
∵PQ⊥AP，
∴∠APB+∠QPC=90°
∠APB+∠BAP=90°
∴∠BAP=∠QPC
∴△ABP∽△PCQ
∴$\frac{BP}{CQ}$=$\frac{AB}{PC}$，即$\frac{x}{y}$=$\frac{4}{4-x}$，
∴y=-$\frac{1}{4}$x²+x=-$\frac{1}{2}$（x-2）²+1（0＜x＜4）；
∴当x=2时，y有最大值1cm．
易知点O的运动轨迹是O′→O→O′，CQ最大时，OO′=$\frac{1}{2}$CQ=$\frac{1}{2}$，
∴点O的运动轨迹的路径的长为2OO′=1，
答答案为1．

点评 本题主要考查正方形的性质、二次函数的应用、三角形的中位线定理等知识，关键在于理解题意运用三角形的相似性质求出y与x之间的函数关系，学会探究点O的运动轨迹．