��Ŀ����
��1��̽�����ȹ۲첢�������и�ʽ���ڿհ״����ϡ���������������=��������ɺ�������⣮
32+42 2��3��4��42+��-5��2 2��4����-5����
��-4��2+��-6��2 2����-4������-6����72+72 2��7��7
���ú���a��b��ʽ�ӱ�ʾ�������ɣ� ��
��2���ã�1���еĽ��ۣ������������⣺
��֪ʵ��a��b����a��0��b��0����a2-ab+b2=4
����ab��ȡֵ��Χ��
����k=a2+ab+b2����k��ȡֵ��Χ��
32+42
��-4��2+��-6��2
���ú���a��b��ʽ�ӱ�ʾ�������ɣ�
��2���ã�1���еĽ��ۣ������������⣺
��֪ʵ��a��b����a��0��b��0����a2-ab+b2=4
����ab��ȡֵ��Χ��
����k=a2+ab+b2����k��ȡֵ��Χ��
���㣺��ȫƽ����ʽ
ר�⣺������
��������1��������֪����ֱ���жϵó������������仯���ɣ�
��2����������֪�ó�ab+4��2ab�������ó�ab��4�����ɵó�ab��ȡֵ��Χ��
��k=a2+ab+b2=��a2+b2��+ab=ab+4+ab=2ab+4�������ó��𰸣�
��2����������֪�ó�ab+4��2ab�������ó�ab��4�����ɵó�ab��ȡֵ��Χ��
��k=a2+ab+b2=��a2+b2��+ab=ab+4+ab=2ab+4�������ó��𰸣�
����⣺��1��32+42��2��3��4��42+��-5��2��2��4����-5����
��-4��2+��-6��2��2����-4������-6����72+72=2��7��7
���ú���a��b��ʽ�ӱ�ʾ�������ɣ�a2+b2��2ab��
�ʴ�Ϊ��������������=��a2+b2��2ab��
��2������a2-ab+b2=4��a2+b2=ab+4��
��a2+b2��2ab����ab+4��2ab��
��ab��4����a=b=2ʱ�Ⱥų�������
�֡�a��0��b��0��
��ab��0����a=0��b=2��a=2��b=0ʱ�Ⱥų�������
��0��ab��4��
��k=a2+ab+b2=��a2+b2��+ab=ab+4+ab=2ab+4��
��0��ab��4����4��2ab+4��12��
��k��ȡֵ��ΧΪ��4��k��12��
��-4��2+��-6��2��2����-4������-6����72+72=2��7��7
���ú���a��b��ʽ�ӱ�ʾ�������ɣ�a2+b2��2ab��
�ʴ�Ϊ��������������=��a2+b2��2ab��
��2������a2-ab+b2=4��a2+b2=ab+4��
��a2+b2��2ab����ab+4��2ab��
��ab��4����a=b=2ʱ�Ⱥų�������
�֡�a��0��b��0��
��ab��0����a=0��b=2��a=2��b=0ʱ�Ⱥų�������
��0��ab��4��
��k=a2+ab+b2=��a2+b2��+ab=ab+4+ab=2ab+4��
��0��ab��4����4��2ab+4��12��
��k��ȡֵ��ΧΪ��4��k��12��
������������Ҫ���������ֱ仯�����Լ���ȫƽ����ʽ��Ӧ�ã��ó�����֮��ı仯�����ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
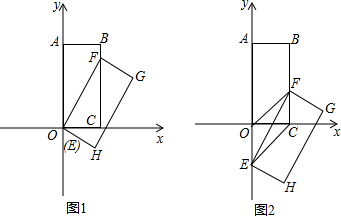
 ��ͼ��ƽ��ֱ������ϵ�У�����ABCD�Ķ���A�����꣨2��4����AB=4��AD=2������������ƽ��m����λ��ʹ���ε���������ǡ��ͬʱ����ij��������������ͼ���ϣ���m=
��ͼ��ƽ��ֱ������ϵ�У�����ABCD�Ķ���A�����꣨2��4����AB=4��AD=2������������ƽ��m����λ��ʹ���ε���������ǡ��ͬʱ����ij��������������ͼ���ϣ���m=