题目内容
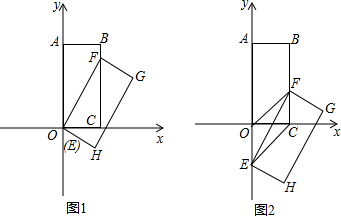
如图1,平面直角坐标系中,四边形OABC是长方形,O为坐标原点,点A(0,4)点C(2,0),将长方形OABC绕点O按顺时针方向旋转30°,得到四边形EFGH,(点E与点O重合).
(1)求点F的坐标,并判断点F是否在线段BC上;
(2)如图2,将四边形EFGH沿y轴向下平移m个单位,当四边形OFCE是平行四边形时,求m的值;
(3)在(2)的基础上,过点O作直线l将?OFCE分为面积比为1:3的两部分,求直线l的解析式.
(1)求点F的坐标,并判断点F是否在线段BC上;
(2)如图2,将四边形EFGH沿y轴向下平移m个单位,当四边形OFCE是平行四边形时,求m的值;
(3)在(2)的基础上,过点O作直线l将?OFCE分为面积比为1:3的两部分,求直线l的解析式.

考点:一次函数综合题
专题:
分析:(1)求一个点的坐标,就需要知道该点到x轴,y轴分别的距离.所以过点F作辅助线垂直与y轴,表示出来F点横坐标的长度是必须的步骤,至于其长度可以利用30°直角三角形的边长特性求解.而判断一个点是否在一条线上,只需求出该线的方程,再判断点的坐标是否满足方程即可.
(2)动点问题关键是找不动的内容,图形在向下平移过程中,都保持FC∥OE,所以根据平行四边形判定的性质,只需再保证FC=OE即可.
(3)面积的分割一般为等底不等高,或者等高不等底.在这个图象中考虑一四象限部分,l只可能出现在OC的上方,下方或者在OC上.当在OC上是,由于OC为?OFCE的对角线,则l将这个四边形分为面积相等的两部分.那么若是面积比为1:3,那么只需让l将△OFC或者△OCE分成相等的两部分即可,即过FC的中点,或者EC的中点.
(2)动点问题关键是找不动的内容,图形在向下平移过程中,都保持FC∥OE,所以根据平行四边形判定的性质,只需再保证FC=OE即可.
(3)面积的分割一般为等底不等高,或者等高不等底.在这个图象中考虑一四象限部分,l只可能出现在OC的上方,下方或者在OC上.当在OC上是,由于OC为?OFCE的对角线,则l将这个四边形分为面积相等的两部分.那么若是面积比为1:3,那么只需让l将△OFC或者△OCE分成相等的两部分即可,即过FC的中点,或者EC的中点.
解答:解:
(1)过点F作FI⊥AO,交AO于点I
在△FIO中,
∵∠FOI=30°,FO=4
∴FI=
FO=
•4=2
IO=
=2
∵F的纵坐标等于IO的长
∴F的坐标为(2,2
)
又 线段BC方程为x=2(0≤y≤4)
∴F在线段BC上
(2)四边形FGHE向下平移m个单位,则其顶点F、E坐标如下:
F(2,2
-m),E(0,-m)
∵O、C坐标分别为:O(0,0),C(2,0)
∴OE=0-(-m)=m,FC=2
-m-0=2
-m
∵四边形OFCE为平行四边形
∴OE=FC,即m=2
-m
∴m=
(3)作△OFC的中线OJ交FC于J,作△OCE的中线OK交CE于K
则S△OFJ=S△OCJ,S△OCK=S△OEK
在?OFCE中,
∵S△OFC=S△OCE
∴S△OFJ:S四边形OJCK
=S△OFJ:(S△OJC+S△OCE)
=S△OFJ:(S△OFJ+2S△OFJ)
=1:3
同理,S△OKE:S四边形OFCK=1:3
∴直线l过O、J两点,或过O、K两点.
∵O(0,0),C(2,0),E(0,-
),F(2,
)
∴J(2,
),K(1,-
)
设直线l的解析式为y=kx+b,
分别代入O、J两点,整理得lOJ:y=
x;
分别代入O、J两点,整理得lOK:y=-
x.

(1)过点F作FI⊥AO,交AO于点I
在△FIO中,
∵∠FOI=30°,FO=4
∴FI=
| 1 |
| 2 |
| 1 |
| 2 |
IO=
| FO2-FI2 |
| 3 |
∵F的纵坐标等于IO的长
∴F的坐标为(2,2
| 3 |
又 线段BC方程为x=2(0≤y≤4)
∴F在线段BC上
(2)四边形FGHE向下平移m个单位,则其顶点F、E坐标如下:
F(2,2
| 3 |
∵O、C坐标分别为:O(0,0),C(2,0)
∴OE=0-(-m)=m,FC=2
| 3 |
| 3 |
∵四边形OFCE为平行四边形
∴OE=FC,即m=2
| 3 |
∴m=
| 3 |
(3)作△OFC的中线OJ交FC于J,作△OCE的中线OK交CE于K
则S△OFJ=S△OCJ,S△OCK=S△OEK
在?OFCE中,
∵S△OFC=S△OCE
∴S△OFJ:S四边形OJCK
=S△OFJ:(S△OJC+S△OCE)
=S△OFJ:(S△OFJ+2S△OFJ)
=1:3
同理,S△OKE:S四边形OFCK=1:3
∴直线l过O、J两点,或过O、K两点.
∵O(0,0),C(2,0),E(0,-
| 3 |
| 3 |
∴J(2,
| ||
| 2 |
| ||
| 2 |
设直线l的解析式为y=kx+b,
分别代入O、J两点,整理得lOJ:y=
| ||
| 4 |
分别代入O、J两点,整理得lOK:y=-
| ||
| 2 |
点评:本题的综合应用比较强,内容涉及到求点左边及直线解析式等.首先学生要对相关概念及其常规求解步骤非常清晰.另外题目还涉及平行四边形的一些性质及图象平移坐标点的变化规律等内容也需要学生知识扎实.最后总结一下本题涉及到的一些常用技巧,一当我们求某个量的时候,最后先作辅助线表示出来再计算,这样容易获得思路.二求动点问题时,找到图形或点运动过程中,什么量是不变的,往往这就会是题目突破的思路.三对于面积分割的问题是我们常常被考察的,基本用到的都是三角形之间的同高不同底,同地不同高的一些性质规律,所以学生需要深入研究熟记这些规律.

练习册系列答案
相关题目
观察下列图形(每幅图中最小的三角形都是全等的),请写出第n个图中最小的三角形的个数有( )个.


| A、4n |
| B、3n-2 |
| C、n4 |
| D、4n-1 |
 如图,平面直角坐标系,A、B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则A1B1的中点为( )
如图,平面直角坐标系,A、B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则A1B1的中点为( )| A、(1,0.5) |
| B、(2,1) |
| C、(2.5,1.5) |
| D、(2,1.5) |
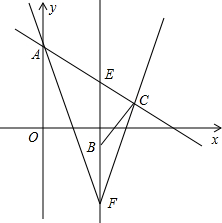 如图,已知点A(0,6),B(4,-2),C(7,
如图,已知点A(0,6),B(4,-2),C(7,