Question

已知抛物线y₁=ax²+bx+c（a≠0）与x轴相交于点A，B（点A，B在原点O两侧），与y轴相交于点C，且点A，C在一次函数y=3x+n的图象上，线段AB长为14，线段OC长为6，当y₁随着x的增大而减小时，求自变量x的取值范围．

Answer 1

考点：抛物线与x轴的交点

专题：

分析：根据OC的长求出n的值为6或-6，然后分①n=6时，求出A的坐标，再根据抛物线的性质求出点B的坐标，求出抛物线的对称轴，然后根据抛物线的对称性写出x的取值范围；②n=-6时，求出A的坐标，再根据抛物线的性质求出点B的坐标，求出抛物线的对称轴，然后根据抛物线的对称性写出x的取值范围．

解答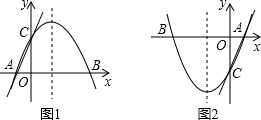：解：根据OC长为6可得一次函数中的n=6或-6 
分类讨论：（1）n=6时，易得如图A（-8，0）
∵抛物线过A、两点，且与x轴交点y=

2

x

，B在原点两侧∴抛物线开口向下，则a＜0
∵AB=14，且A（-8，0），
∴B（6，0）
而A、B，关于对称轴对称∴对称轴直线x=-1 
要使y₁随着x的增大而减小，且a＜0，
∴x≥-1（等号不取也可以）；

（2）n=-6时，易得如图A（8，0）
∵抛物线过A、C两点，且与x轴交点A，B在原点两侧∴抛物线开口向上，则a＞0
∵AB=14，且A（8，0），
∴B（-6，0）
而A，B关于对称轴对称
∴对称轴直线x=1
要使y₁随着x的增大而减小，且a＞0，
∴x≤1（等号不取也可以）．

点评：本题考查了二次函数的性质，主要利用了二次函数的对称性，难点在于要分情况讨论．