题目内容
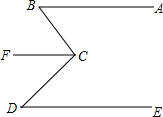 如图,已知AB∥CF,AB∥DE,求证:∠B+∠D=∠BCF+∠DCF.
如图,已知AB∥CF,AB∥DE,求证:∠B+∠D=∠BCF+∠DCF.证明:∵AB∥CF(已知),
∴∠
∵AB∥CF,AB∥DE(已知)
∴CF∥DE(
∴∠
∴∠B+∠D=∠BCF+∠DCF(等式性质)
考点:平行线的判定与性质
专题:推理填空题
分析:根据平行于同一条直线的两条直线平行,得到CF∥DE;然后根据平行线的性质,两直线平行,内错角相等得出∠B=∠BCF,∠D=∠DCF;再利用等式的性质即可得出∠B+∠D=∠BCF+∠DCF.
解答:证明:∵AB∥CF(已知),
∴∠B=∠BCF(两直线平行,内错角相等),
∵AB∥CF,AB∥DE(已知),
∴CF∥DE(平行于同一条直线的两条直线平行),
∴∠D=∠DCF(两直线平行,内错角相等),
∴∠B+∠D=∠BCF+∠DCF(等式性质).
故答案为:B;BCF;两直线平行,内错角相等;平行于同一条直线的两条直线平行;D;DCF;两直线平行,内错角相等.
∴∠B=∠BCF(两直线平行,内错角相等),
∵AB∥CF,AB∥DE(已知),
∴CF∥DE(平行于同一条直线的两条直线平行),
∴∠D=∠DCF(两直线平行,内错角相等),
∴∠B+∠D=∠BCF+∠DCF(等式性质).
故答案为:B;BCF;两直线平行,内错角相等;平行于同一条直线的两条直线平行;D;DCF;两直线平行,内错角相等.
点评:此题考查了平行线的性质和判定,解答此题的关键是注意平行线的性质和判定定理的综合运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数y=x2-2015x+2014与x轴交点是(m,0),(n,0),则(m2-2014m+2014)(n2-2014n+2014)的值是( )
| A、2013 | B、2014 |
| C、2015 | D、2016 |
 如图,已知点A(-4,4),点B为x轴的负半轴上的点,C为函数y=
如图,已知点A(-4,4),点B为x轴的负半轴上的点,C为函数y=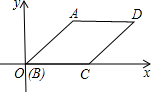 如图,?ABCD放入直角坐标系,BC在x轴上,且AB=4,BC=3,∠ABC=45°,则点D的坐标为
如图,?ABCD放入直角坐标系,BC在x轴上,且AB=4,BC=3,∠ABC=45°,则点D的坐标为 已知四边形OACB的四个顶点分别是O(0,0),B(3,3),C(6,0),A(3,-3).在直角坐标系中画出这个四边形,并求这个四边形的面积.
已知四边形OACB的四个顶点分别是O(0,0),B(3,3),C(6,0),A(3,-3).在直角坐标系中画出这个四边形,并求这个四边形的面积.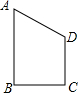 四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=3,AB=4,把梯形ABCD分别绕直线
四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=3,AB=4,把梯形ABCD分别绕直线