题目内容
 如图,已知点A(-4,4),点B为x轴的负半轴上的点,C为函数y=
如图,已知点A(-4,4),点B为x轴的负半轴上的点,C为函数y=| 4 |
| x |
考点:反比例函数综合题
专题:
分析:作AD⊥x轴于D,CE⊥x轴于E,先证得△ADB≌△BEC,从而求得AD=BE,DB=CE,设B(m,0),根据A的坐标即可得出C(4+m,4+m),代入函数的解析式即可求得点B和点C的坐标.
解答: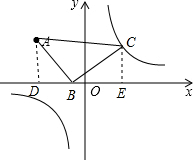 解:存在;
解:存在;
理由:如图,作AD⊥x轴于D,CE⊥x轴于E,
∵△ABC为等腰直角三角形,且∠ABC=90°,
∴∠ABD+∠CBE=90°,
∵∠ABD+∠DAB=90°,
∴∠DAB=∠CBE,
在△ADB和△BEC中,
,
∴△ADB≌△BEC(AAS),
∴AD=BE,DB=CE,
设B(m,0),
∵点A(-4,4),
∴DB=4+m,-m+OE=4,
∴CE=4+m,OE=4+m,
∴C(4+m,4+m),
∵C为函数y=
的图象上的点,
∴4+m=
,
解得m=-2或m=-6,
∴B的坐标为(-2,0)或(-6,0),C的坐标为(2,2)或(-2,-2).
 解:存在;
解:存在;理由:如图,作AD⊥x轴于D,CE⊥x轴于E,
∵△ABC为等腰直角三角形,且∠ABC=90°,
∴∠ABD+∠CBE=90°,
∵∠ABD+∠DAB=90°,
∴∠DAB=∠CBE,
在△ADB和△BEC中,
|
∴△ADB≌△BEC(AAS),
∴AD=BE,DB=CE,
设B(m,0),
∵点A(-4,4),
∴DB=4+m,-m+OE=4,
∴CE=4+m,OE=4+m,
∴C(4+m,4+m),
∵C为函数y=
| 4 |
| x |
∴4+m=
| 4 |
| 4+m |
解得m=-2或m=-6,
∴B的坐标为(-2,0)或(-6,0),C的坐标为(2,2)或(-2,-2).
点评:本题是反比例函数的综合题,考查了三角形全等的判定和性质,等腰直角三角形的性质,函数图象上点的坐标特征,作出辅助线构建全等三角形是本题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
方程x2=9的根是( )
| A、x=3 |
| B、x=-3 |
| C、x1=3,x2=-3 |
| D、x1=x2=3 |
⊙O1与⊙O2的圆心距为6,且两圆半径是方程x2-6x+5=0的两根,则两圆的位置关系为( )
| A、内切 | B、外切 | C、外离 | D、相交 |
 如图,一副三角板的两个直角顶点重合在一起.
如图,一副三角板的两个直角顶点重合在一起.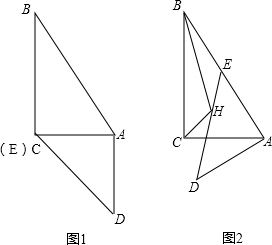 已知如图1,Rt△ABC和Rt△ADE的直角边AC和AE重叠在一起,AD=AE,∠B=30°,∠DAE=∠ACB=90°.
已知如图1,Rt△ABC和Rt△ADE的直角边AC和AE重叠在一起,AD=AE,∠B=30°,∠DAE=∠ACB=90°.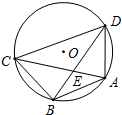 如图,已知A、B、C、D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD、AD.
如图,已知A、B、C、D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD、AD.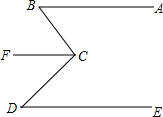 如图,已知AB∥CF,AB∥DE,求证:∠B+∠D=∠BCF+∠DCF.
如图,已知AB∥CF,AB∥DE,求证:∠B+∠D=∠BCF+∠DCF.