题目内容
如图,小刚同学在广场上观测新华书店楼房墙上的电子屏幕CD,点A是小刚的眼睛,测得屏幕下端D处的仰角为28°,然后他正对屏幕方向前进了6米到达B处,又测得该屏幕上端C处的仰角为47°,延长AB与楼房垂直相交于点E,测得BE=21米,请你帮小刚求出该屏幕上端与下端之间的距离CD.(精确到0.1米)


考点:解直角三角形的应用-仰角俯角问题
专题:
分析:利用47°,28°的正切值,即可求得CE、DE的长,CE减去DE长即为广告屏幕上端与下端之间的距离CD.
解答:解:∵∠CBE=47°,CE⊥AE,
∴CE:BE=tan47°,
∵BE=21米,
∴CE=BE•tan47°,
∴CE≈21×1.072=22.512米,
∵∠DAE=28°,DE⊥AE,
∴DE:AE=tan28°,
∵AB=6米,
∴AE=27米,
∴DE=AE•tan28°,
∴CE≈27×0.532=14.364米,
∴CD=CE-DE=22.512-14.364=8.148≈8.1.
答:广告屏幕上端与下端之间的距离CD约为8.1m.
∴CE:BE=tan47°,
∵BE=21米,
∴CE=BE•tan47°,
∴CE≈21×1.072=22.512米,
∵∠DAE=28°,DE⊥AE,
∴DE:AE=tan28°,
∵AB=6米,
∴AE=27米,
∴DE=AE•tan28°,
∴CE≈27×0.532=14.364米,
∴CD=CE-DE=22.512-14.364=8.148≈8.1.
答:广告屏幕上端与下端之间的距离CD约为8.1m.
点评:本题考查了仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形;难点是充分找到并运用题中相等的线段.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
⊙O1与⊙O2的圆心距为6,且两圆半径是方程x2-6x+5=0的两根,则两圆的位置关系为( )
| A、内切 | B、外切 | C、外离 | D、相交 |
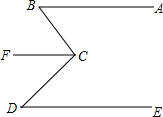 如图,已知AB∥CF,AB∥DE,求证:∠B+∠D=∠BCF+∠DCF.
如图,已知AB∥CF,AB∥DE,求证:∠B+∠D=∠BCF+∠DCF. 求出下列图中x的值.
求出下列图中x的值.