题目内容
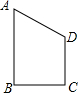 四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=3,AB=4,把梯形ABCD分别绕直线
四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=3,AB=4,把梯形ABCD分别绕直线AB,CD旋转一周,所得几何体的表面积分别为S1,S2,则|S1-S2|=
考点:圆锥的计算,点、线、面、体
专题:
分析:梯形ABCD分别绕直线AB,CD旋转一周所得的几何体的表面积的差就是AB和CD旋转一周形成的圆柱的侧面的差.
解答:解:绕AB旋转一周形成的圆柱的侧面的面积是:2π×3×2=12π;
绕CD旋转一周形成的圆柱的侧面的面积是:2π×2×4=16π,
则|S1-S2|=4π.
故答案是:4π.
绕CD旋转一周形成的圆柱的侧面的面积是:2π×2×4=16π,
则|S1-S2|=4π.
故答案是:4π.
点评:本题考查了图形的旋转,理解梯形ABCD分别绕直线AB,CD旋转一周所得的几何体的表面积的差就是AB和CD旋转一周形成的圆柱的侧面的差是关键.

练习册系列答案
相关题目
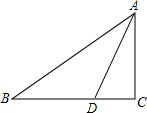 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,CD=4,则点D到AB的距离是( )
如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,CD=4,则点D到AB的距离是( )| A、4 | B、2 | C、3 | D、6 |
⊙O1与⊙O2的圆心距为6,且两圆半径是方程x2-6x+5=0的两根,则两圆的位置关系为( )
| A、内切 | B、外切 | C、外离 | D、相交 |
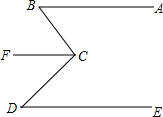 如图,已知AB∥CF,AB∥DE,求证:∠B+∠D=∠BCF+∠DCF.
如图,已知AB∥CF,AB∥DE,求证:∠B+∠D=∠BCF+∠DCF.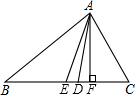 如图,在△ABC中,AE是中线,AD是角平分线,AF是高,则:
如图,在△ABC中,AE是中线,AD是角平分线,AF是高,则: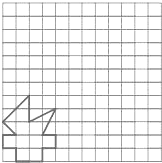 为迎接2009年10月11日第十一届全运会,山东体育迷小强利用网格设计了一个“火炬”图案,请你帮帮他:将“火炬”图案先向右平移7格,再向上平移6格,画出平移后的图案.
为迎接2009年10月11日第十一届全运会,山东体育迷小强利用网格设计了一个“火炬”图案,请你帮帮他:将“火炬”图案先向右平移7格,再向上平移6格,画出平移后的图案.