Question

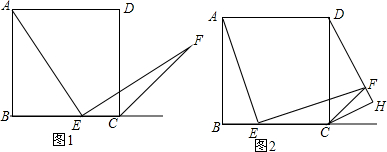
5．已知：AB⊥BD，ED⊥BD，C是BD上一点，且AC=EC，AC⊥EC．求证：BD=AB+ED．

Answer 1

分析 求出∠A=∠2，根据AAS证△ABC≌△CDE，推出AB=CD，BC=ED，代入求出即可．

解答 证明：∠ABC=90°，∠CDE=90°，AC⊥CE，

∴∠ACE=90°，
∴∠1+∠2=90°，∠1+∠A=90°，
∴∠2=∠A，
在△ABC和△CDE中，
$\left\{\begin{array}{l}{∠ABC=∠EDC}\\{∠A=∠2}\\{AC=EC}\end{array}\right.$，
∴△ABC≌△CDE（AAS），
∴AB=CD，BC=ED，
∵BD=BC+CD，
∴AB+ED=BD．

点评 本题考查了三角形的内角和定理，全等三角形的性质和判定，关键是推出△ABC≌△CDE，全等三角形的判定定理有SAS，ASA，AAS，SSS．