题目内容
7.已知点(-1,y1)、(2,y2)、(π,y3)在双曲线y=$\frac{{k}^{2}+1}{x}$上,则下列关系式正确的是( )| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y2>y3>y1 | D. | y3>y1>y2 |
分析 先根据反比例函数的解析式判断出函数图象所在的象限及其增减性,再根据各点横坐标的值即可得出结论.
解答 解:∵反比例函数y=$\frac{{k}^{2}+1}{x}$中,k2+1>0,
∴此函数图象的两个分支分别位于一三象限,且在每一象限内y随x的增大而减小.
∵-1<0,0<2<π,
∴点(-1,y1)在第三象限,点(2,y2)、(π,y3)在第一象限,
∴y1<y3<y2.
故选C.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数的增减性是解答此题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
 如图,∠AOC与∠BOC的度数比为5:2,OD平分∠AOB,若∠COD=15°,求∠AOB的度数.
如图,∠AOC与∠BOC的度数比为5:2,OD平分∠AOB,若∠COD=15°,求∠AOB的度数.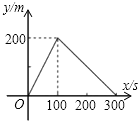
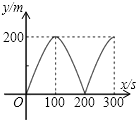
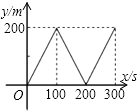
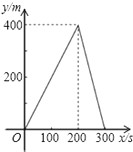
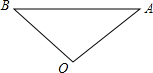 如图,爸爸从家(点O)出发,沿着等腰三角形AOB的边OA→AB→BO的路径去匀速散步,其中OA=OB.设爸爸距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )
如图,爸爸从家(点O)出发,沿着等腰三角形AOB的边OA→AB→BO的路径去匀速散步,其中OA=OB.设爸爸距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )



 如图1,C地位于A,B两地之间,甲步行直接从C地前往B地;乙骑自行车由C地先回A地,再从A地前往B地(在A地停留时间忽略不计).已知两人同时出发且速度不变,乙的速度是甲的$\frac{5}{2}$倍,设出发xmin后甲、乙两人离C地的距离分别为y1m,y2m,图②中线段OM表示y1与x的函数图象.
如图1,C地位于A,B两地之间,甲步行直接从C地前往B地;乙骑自行车由C地先回A地,再从A地前往B地(在A地停留时间忽略不计).已知两人同时出发且速度不变,乙的速度是甲的$\frac{5}{2}$倍,设出发xmin后甲、乙两人离C地的距离分别为y1m,y2m,图②中线段OM表示y1与x的函数图象. 已知,如图,直线AB与CD相交于点O,OE平分∠AOC,若∠EOC=25°,则∠BOD的度数为50°.
已知,如图,直线AB与CD相交于点O,OE平分∠AOC,若∠EOC=25°,则∠BOD的度数为50°.