题目内容
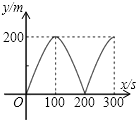
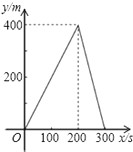
11.如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动.设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )
| A. | AE=6cm | B. | sin∠EBC=0.8 | ||
| C. | 当0<t≤10时,y=0.4t2 | D. | 当t=12s时,△PBQ是等腰三角形 |
分析 根据图象可以得到BC和BE的长度,以及DE的长度,根据图2中y的值可以求得CD的长,从而可以得到AE的长,从而可以判断A;
作辅助线EF⊥BC于点F,由于EF=CD的长,从而可以得到sin∠EBC的值,可以判断B;
根据函数图象可以求得在0<t≤10时,求得△BPQ底边BQ上的高,从而可以得到△BPQ的面积,从而可以判断C;
根据题意可以分别求得在t=12时,BQ、QP、PB的长,从而判断D.
解答 解:A、由图象可知,
BC=BE=10,DE=14-10=4,
∴AD=10,
∴AE=AD-DE=10-4=6cm,故A正确;
B、作EF⊥BC于点F,作PM⊥BQ于点M,如下图所示,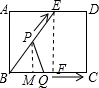
由图象可知,三角形PBQ的最大面积为40,
∴$\frac{1}{2}$BC•EF=$\frac{1}{2}$×10•EF=40,
解得EF=8,
∴sin∠EBC=$\frac{EF}{BE}$=$\frac{8}{10}$=0.8,故B正确;
C、当0<t≤10时,△BMP∽△BFE,
∴$\frac{PM}{EF}$=$\frac{BP}{BE}$,即$\frac{PM}{8}$=$\frac{t}{10}$,
解得PM=$\frac{4}{5}$t,
∴△BPQ的面积=$\frac{1}{2}$BQ•PM=$\frac{1}{2}$•t•$\frac{4}{5}$t=0.4t2,
即y=0.4t2,故C正确;
D、当t=12时,BQ=10,PQ=$\sqrt{Q{D}^{2}+D{P}^{2}}$=$\sqrt{{8}^{2}+{2}^{2}}$=2$\sqrt{17}$,BP=$\sqrt{A{B}^{2}+A{P}^{2}}$=$\sqrt{{8}^{2}+{8}^{2}}$=8$\sqrt{2}$,
∴△BPQ不是等腰三角形,故D错误;
故选D.
点评 本题考查动点问题的函数图象,需要结合几何图形与函数图象,认真分析动点的运动过程.突破点在于正确判断出BC=BE=10cm.

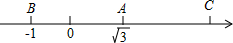 如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )
如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )| A. | 1+$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 2$\sqrt{3}$-1 | D. | 2$\sqrt{3}$+1 |
 某工厂投入生产一种机器,当该机器生产数量至少10台,但不超过70台,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如表:
某工厂投入生产一种机器,当该机器生产数量至少10台,但不超过70台,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如表:| x(单位:台) | 10 | 20 | 30 |
| y(单位:万元∕台) | 60 | 55 | 50 |
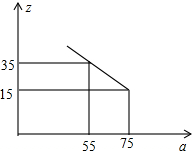
(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系,求z与a之间的函数关系式.
(3)若该厂第一个月生产这种机器50台,且第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价-成本)
| A. | k>0,b>0 | B. | k<0,b>0 | C. | k>0,b<0 | D. | k<0,b<0 |
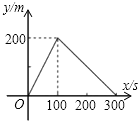
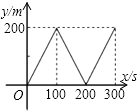
 如图1,C地位于A,B两地之间,甲步行直接从C地前往B地;乙骑自行车由C地先回A地,再从A地前往B地(在A地停留时间忽略不计).已知两人同时出发且速度不变,乙的速度是甲的$\frac{5}{2}$倍,设出发xmin后甲、乙两人离C地的距离分别为y1m,y2m,图②中线段OM表示y1与x的函数图象.
如图1,C地位于A,B两地之间,甲步行直接从C地前往B地;乙骑自行车由C地先回A地,再从A地前往B地(在A地停留时间忽略不计).已知两人同时出发且速度不变,乙的速度是甲的$\frac{5}{2}$倍,设出发xmin后甲、乙两人离C地的距离分别为y1m,y2m,图②中线段OM表示y1与x的函数图象.