题目内容
2. 如图,在△ABC中,BD是角平分线,EF垂直平分BD于点O,请指出图中的全等三角形,并选择一对全等三角形加以证明.
如图,在△ABC中,BD是角平分线,EF垂直平分BD于点O,请指出图中的全等三角形,并选择一对全等三角形加以证明.
分析 根据线段垂直平分线得出BE=DE,DF=BF,OD=OB,根据等腰三角形性质和角平分线定义求出∠EBO=∠EDO=∠FBO=∠FDO,根据全等三角形的判定逐个推出即可.
解答 解:全等三角形有△BED≌△DFB,△DEF≌△BFE,△DOE≌△BOF,△BOE≌△DOF,
选△DEF≌△BFE,
证明:∵EF垂直平分BD,
∴BE=DE,DF=BF,
在△DEF和△BFE中,
$\left\{\begin{array}{l}{DF=BF}\\{DE=BE}\\{EF=EF}\end{array}\right.$,
∴△DEF≌△BFE(SSS).
点评 本题考查了角平分线定义,线段垂直平分线性质,全等三角形的判定的应用,能推出判定三角形全等的三个条件是解此题的关键.

练习册系列答案
相关题目
12.等腰三角形的周长为10,底边长y与腰x的函数关系式是y=10-2x,则自变量x的取值范围是( )
| A. | x>0 | B. | x<5 | C. | 0<x<5 | D. | 2.5<x<5 |
13.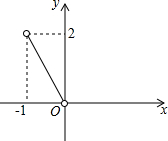 已知函数图象如图所示,则此函数解析式为( )
已知函数图象如图所示,则此函数解析式为( )
 已知函数图象如图所示,则此函数解析式为( )
已知函数图象如图所示,则此函数解析式为( )| A. | y=-2x | B. | y=-2x(-1<x<0) | C. | y=-$\frac{1}{2}$x | D. | y=-$\frac{1}{2}$x(-1<x<0) |
11.若a≠b,下列各式中不能成立的是( )
| A. | (a+b)2=(-a-b)2 | B. | (-a-b)(a-b)=(b+a)(b-a) | C. | (a-b)2n=(b-a)2n | D. | (a-b)3=(b-a)3 |
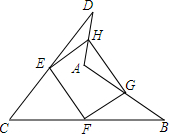 如图所示,点E,F,G,H分别是CD,BC,AB,DA的中点,求证:四边形EFGH是平行四边形.
如图所示,点E,F,G,H分别是CD,BC,AB,DA的中点,求证:四边形EFGH是平行四边形.