题目内容
12.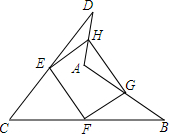 如图所示,点E,F,G,H分别是CD,BC,AB,DA的中点,求证:四边形EFGH是平行四边形.
如图所示,点E,F,G,H分别是CD,BC,AB,DA的中点,求证:四边形EFGH是平行四边形.
分析 证明EF是△BCD的中位线,GH是△ABD的中位线,由三角形中位线定理得出EF∥BD,EF=$\frac{1}{2}$BD,GH∥BD,GH=$\frac{1}{2}$BD,得出EF∥GH,EF=GH,即可得出结论.
解答 证明:连接BD.如图所示: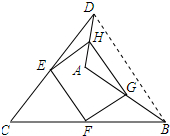
∵点E,F,G,H分别是CD,BC,AB,DA的中点,
∴EF是△BCD的中位线,GH是△ABD的中位线,
∴EF∥BD,EF=$\frac{1}{2}$BD,GH∥BD,GH=$\frac{1}{2}$BD,
∴EF∥GH,EF=GH,
∴四边形EFGH是平行四边形.
点评 本题考查了平行四边形的判定方法、三角形中位线定理;熟练掌握平行四边形的判定方法,证明三角形中位线是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,BD是角平分线,EF垂直平分BD于点O,请指出图中的全等三角形,并选择一对全等三角形加以证明.
如图,在△ABC中,BD是角平分线,EF垂直平分BD于点O,请指出图中的全等三角形,并选择一对全等三角形加以证明.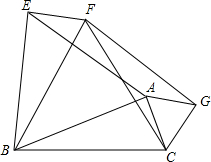 如图,以△ABC的三边为一边的BC的同侧作等边三角形△ABE,△BCF,△ACG.求证:四边形AEFG是平行四边形.
如图,以△ABC的三边为一边的BC的同侧作等边三角形△ABE,△BCF,△ACG.求证:四边形AEFG是平行四边形. (1)请在如图中的坐标系中画出函数y=x2-x和y=x+1的图象;
(1)请在如图中的坐标系中画出函数y=x2-x和y=x+1的图象; 知图,有一块长80cm,宽60cm的长方形硬纸片,在四角各剪去一个同样的小正方形,用剩余部分做成一个底面积为1500cm2的无盖的长方体盒子,求剪去的小正方形的边长.
知图,有一块长80cm,宽60cm的长方形硬纸片,在四角各剪去一个同样的小正方形,用剩余部分做成一个底面积为1500cm2的无盖的长方体盒子,求剪去的小正方形的边长.