题目内容
如图，平行四边形ABCD中，点E为AB边的中点，点F为BC边的三等分点，连接AF、DE相交于点G，则| AG |
| FG |
考点：平行线分线段成比例,平行四边形的性质
专题：
分析：根据已知分别延长CB，DE两射线相交于点R，过点B作BW∥AF于点W，得出AD=BR，AG=BW，再利用平行线分线段成比例定理得出
=
=
，进而求出即可．
| AG |
| GF |
| BW |
| GF |
| RB |
| RF |
解答：解：分别延长CB，DE两射线相交于点R，过点B作BW∥AF，交DR于点W，
∵在平行四边形ABCD中，
∴AD∥BR，
∴∠ADR=∠R，
∵E为AB的中点，即AE=BE，
∴在△AED和△BER中，
，
∴△AED≌△BER（AAS），
∴AD=BR，
∵AG∥BW，
∴∠EAG=∠EBW，
∴在△AEG和△BWE中，
，
∴△AEG≌△BWE（ASA），
∴AG=BW，
∵BW∥GF，
∴
=
=
，
∵点F为BC边的三等分点，
∴则
的值是：
=
，
故答案为：
．
∵在平行四边形ABCD中，
∴AD∥BR，
∴∠ADR=∠R，
∵E为AB的中点，即AE=BE，
∴在△AED和△BER中，
|
∴△AED≌△BER（AAS），
∴AD=BR，
∵AG∥BW，
∴∠EAG=∠EBW，
∴在△AEG和△BWE中，
|
∴△AEG≌△BWE（ASA），
∴AG=BW，
∵BW∥GF，
∴
| AG |
| GF |
| BW |
| GF |
| RB |
| RF |
∵点F为BC边的三等分点，
∴则
| AG |
| FG |
| AD | ||
AD+
|
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
点评：此题主要考查了平行线分线段成比例定理以及平行线的性质，正确作出辅助线，转化线段关系是解题关键．
练习册系列答案
小学教材完全解读系列答案
相关题目
在△ABC中，AB=20cm，AC=16cm，点P从A点出发，沿AB方向以每秒4cm的速度向B点运动，同时点Q从C点出发，沿CA方向以每秒2cm的速度向A点运动，当P到达B点时，P、Q两点都停止运动，设运动时间为t秒，求t为何值时，以点A、P、Q为顶点的三角形与△ABC相似？
已知△ABC中，AC=6，D是AC的中点，BD=要使
、
、（2x-4）0三个式子都有意义，则x的取值范围应为（ ）
| x+1 |
| 1 | ||
|
A、x＞
| ||
| B、x≥-1且x≠2 | ||
C、x＞
| ||
D、
|
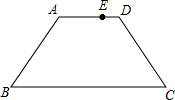如图在梯形ABCD中AB=CD=5，AD=7，BC=13，E点在AD上，且AE=4，动点P从D出发沿着梯形的周界依次经过C、B最后到达A，设此过程中P点走过的距离为x，△APE的面积为y，把y表示成x的函数，并且画出图象．
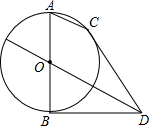已知：如图，AB为⊙O的直径，弦AC∥OD，BD切⊙O于B，连接CD，