题目内容
已知△ABC中，AC=6，D是AC的中点，BD=2| 2 |
考点：相似三角形的判定与性质
专题：
分析：由∠ADB=∠ABC，∠A是公共角，易得△ADB∽△ABC，根据相似三角形的对应边成比例，可得
=
，
=
，又由AC=6，D是AC的中点，可求得AB的长，继而求得BC的长．
| AD |
| AB |
| AB |
| AC |
| AD |
| AB |
| BD |
| BC |
解答：解：∵△ABC中，AC=6，D是AC的中点，
∴AD=
AC=3，
∵∠ADB=∠ABC，∠A是公共角，
∴△ADB∽△ABC，
∴
=
，
=
，
∴AB2=AD•AC=3×6=18，
∴AB=3
，
∵BD=2
，
∴
=
，
∴BC=4．
故答案为：4．
∴AD=
| 1 |
| 2 |
∵∠ADB=∠ABC，∠A是公共角，
∴△ADB∽△ABC，
∴
| AD |
| AB |
| AB |
| AC |
| AD |
| AB |
| BD |
| BC |
∴AB2=AD•AC=3×6=18，
∴AB=3
| 2 |
∵BD=2
| 2 |
∴
| 3 | ||
3
|
2
| ||
| BC |
∴BC=4．
故答案为：4．
点评：此题考查了相似三角形的判定与性质．此题难度适中，注意掌握有两角对应相等的三角形相似与相似三角形的对应边成比例定理的应用是解此题的关键．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
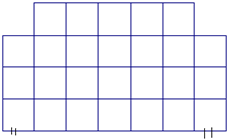一展览馆有26间展室，图中每个方格代表一个展室，每相邻展室有门相同，出口、入口如图所示．问：能否找到一条从入口到出口的参观路线，使不重复不遗漏地走过每一间展室？
在面积为1的△ABC中，P为边BC上的中点，点Q在边AC上，且AQ=2QC，连接AP，BQ相交于点R，求：△ABR的面积？若x2+2（m-3）x+25是一个完全平方式，则m的值为（ ）
| A、6或-3 | B、8或-2 |
| C、8 | D、-5或3 |
如图，平行四边形ABCD中，点E为AB边的中点，点F为BC边的三等分点，连接AF、DE相交于点G，则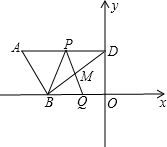
度向点D运动，到达点D后停止，点P、Q同时出发，BD与PQ相交于点M，设运动的时间为t秒．