题目内容
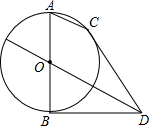 已知:如图,AB为⊙O的直径,弦AC∥OD,BD切⊙O于B,连接CD,
已知:如图,AB为⊙O的直径,弦AC∥OD,BD切⊙O于B,连接CD,(1)求证:CD是⊙O的切线;
(2)若AC=2,OD=6,求⊙O的半径.
考点:切线的判定与性质
专题:
分析:(1)连接OC.欲证CD是⊙O的切线,只需证明OC⊥CD即可;
(2)连接BC交OD于E,先证明△OBE∽△ODB或△ABC∽△ODB,再根据相似三角形的性质及中位线的性质,即可求出⊙O的半径.
(2)连接BC交OD于E,先证明△OBE∽△ODB或△ABC∽△ODB,再根据相似三角形的性质及中位线的性质,即可求出⊙O的半径.
解答: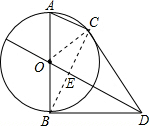 (1)证明:如图,连接OC.
(1)证明:如图,连接OC.
∵OD∥AC(已知),
∴∠COD=∠ACO(两直线平行,内错角相等),∠CAO=∠DOB(两直线平行,同位角相等).(3分)
又∵∠ACO=∠CAO(等边对等角),
∴∠COD=∠DOB(等量代换);
∵OD=OD,OC=OB,
∴△COD≌△BOD(SAS)
∴∠OCD=∠OBD(全等三角形的对应角相等);
∵BD是⊙O的切线,
∴∠OBD=90°,
∴∠OCD=90°,
∴OC⊥CD,即CD是⊙O的切线;
(2)解:连接BC交OD于E.
∵CD和BD都是⊙O的切线,
∴CD=BD,∠CDO=∠BDO;
∴BC⊥OD,BE=CE,∠OBD=90°
∴△OBE∽△ODB
∴OB:OD=OE:OB (相似三角形的对应边成比例);
由BE=CE,OA=OB,
得OE为△ABC的中位线,
即OE=
AC=1,
∴OB:6=1:OB 得OB=±
(舍负)
∴⊙O的半径为
.
 (1)证明:如图,连接OC.
(1)证明:如图,连接OC.∵OD∥AC(已知),
∴∠COD=∠ACO(两直线平行,内错角相等),∠CAO=∠DOB(两直线平行,同位角相等).(3分)
又∵∠ACO=∠CAO(等边对等角),
∴∠COD=∠DOB(等量代换);
∵OD=OD,OC=OB,
∴△COD≌△BOD(SAS)
∴∠OCD=∠OBD(全等三角形的对应角相等);
∵BD是⊙O的切线,
∴∠OBD=90°,
∴∠OCD=90°,
∴OC⊥CD,即CD是⊙O的切线;
(2)解:连接BC交OD于E.
∵CD和BD都是⊙O的切线,
∴CD=BD,∠CDO=∠BDO;
∴BC⊥OD,BE=CE,∠OBD=90°
∴△OBE∽△ODB
∴OB:OD=OE:OB (相似三角形的对应边成比例);
由BE=CE,OA=OB,
得OE为△ABC的中位线,
即OE=
| 1 |
| 2 |
∴OB:6=1:OB 得OB=±
| 6 |
∴⊙O的半径为
| 6 |
点评:本题考查了切线的判定与性质.在解答(2)时,注意三角形中位线定义的运用.

练习册系列答案
相关题目
已知关于x的方程x2-4x+5+a•(
+2)=0,若a为正实数,则下列判断正确的是( )
| 1 |
| x |
| A、有三个不等实数根 |
| B、有两个不等实数根 |
| C、有一个实数根 |
| D、无实数根 |
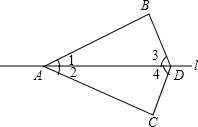 如图,A、D是直线l上两点,B、C两点位于直线l的两侧,若∠1=∠2,则添加下列哪一个条件后,不能保证△ABD≌△ACD( )
如图,A、D是直线l上两点,B、C两点位于直线l的两侧,若∠1=∠2,则添加下列哪一个条件后,不能保证△ABD≌△ACD( )| A、AB=AC |
| B、∠3=∠4 |
| C、∠B=∠C |
| D、BD=CD |
 如图,平行四边形ABCD中,点E为AB边的中点,点F为BC边的三等分点,连接AF、DE相交于点G,则
如图,平行四边形ABCD中,点E为AB边的中点,点F为BC边的三等分点,连接AF、DE相交于点G,则 度向点D运动,到达点D后停止,点P、Q同时出发,BD与PQ相交于点M,设运动的时间为t秒.
度向点D运动,到达点D后停止,点P、Q同时出发,BD与PQ相交于点M,设运动的时间为t秒. 菱形,要求菱形的顶点均在格点上.
菱形,要求菱形的顶点均在格点上. 如图,在锐角△ABC中,CD,BE分别是AB,AC上的高,且CD,BE交于点P,若∠A=80°,∠BPC的度数是
如图,在锐角△ABC中,CD,BE分别是AB,AC上的高,且CD,BE交于点P,若∠A=80°,∠BPC的度数是 如图,等腰直角三角形ABD,点C是直角边AD上的动点,连接CB.现在将点C绕点A逆时针方向旋转90°得点E,再将点C绕点B顺时针方向旋转90°得点F.如果AD=BD=
如图,等腰直角三角形ABD,点C是直角边AD上的动点,连接CB.现在将点C绕点A逆时针方向旋转90°得点E,再将点C绕点B顺时针方向旋转90°得点F.如果AD=BD=