题目内容
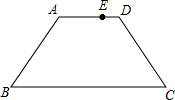 如图在梯形ABCD中AB=CD=5,AD=7,BC=13,E点在AD上,且AE=4,动点P从D出发沿着梯形的周界依次经过C、B最后到达A,设此过程中P点走过的距离为x,△APE的面积为y,把y表示成x的函数,并且画出图象.
如图在梯形ABCD中AB=CD=5,AD=7,BC=13,E点在AD上,且AE=4,动点P从D出发沿着梯形的周界依次经过C、B最后到达A,设此过程中P点走过的距离为x,△APE的面积为y,把y表示成x的函数,并且画出图象.考点:动点问题的函数图象
专题:
分析:此题分三种情况:①当P在CD上时,②当P在BC上时,③当P在AB上时,分别求出解析式,根据解析式画出图象即可.
解答:解:这道题可以分三种情况讨论:
①当P在CD上时,0≤x≤5,过点P作PH⊥AD交AD的延长线与H,过点D作DM⊥BC交BC与点M,
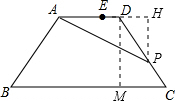
已知AD=7,BC=13,易知:MC=
=3,
又AB=CD=5,根据勾股定理可得DM=4,
∵AD∥BC,
∴∠PDH=∠C,
∴PH=PD•sin∠C=x•sin∠C=
=
x,
∴y=
AE•PH=
x.
②当P在BC上时,5≤x≤18,y=
•AE•DM=8,
③当P在AB上时,18≤x≤23,AP=(AB+BC+CD)-x=23-x,
由①同理可得:y=
×4×(23-x)×sin∠C=
(184-8x).
所以y=,
,
综上得所求的函数图象为: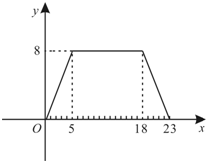
①当P在CD上时,0≤x≤5,过点P作PH⊥AD交AD的延长线与H,过点D作DM⊥BC交BC与点M,

已知AD=7,BC=13,易知:MC=
| 13-7 |
| 2 |
又AB=CD=5,根据勾股定理可得DM=4,
∵AD∥BC,
∴∠PDH=∠C,
∴PH=PD•sin∠C=x•sin∠C=
| DM |
| CD |
| 4 |
| 5 |
∴y=
| 1 |
| 2 |
| 8 |
| 5 |
②当P在BC上时,5≤x≤18,y=
| 1 |
| 2 |
③当P在AB上时,18≤x≤23,AP=(AB+BC+CD)-x=23-x,
由①同理可得:y=
| 1 |
| 2 |
| 1 |
| 5 |
所以y=,
|
综上得所求的函数图象为:

点评:本题考查了动点问题的函数图象,解题关键是对等腰梯形及三角形面积公式的熟练运用,难度适中,注意要分三种情况:P在CD上、P在BC上和P在AB上进行讨论.

练习册系列答案
相关题目
一件衣服以220元出售,可获利10%,则这件衣服的进价是( )
| A、110元 | B、180元 |
| C、198元 | D、200元 |
边长为整数,周长为20的等腰三角形个数是( )
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,平行四边形ABCD中,点E为AB边的中点,点F为BC边的三等分点,连接AF、DE相交于点G,则
如图,平行四边形ABCD中,点E为AB边的中点,点F为BC边的三等分点,连接AF、DE相交于点G,则 如图,已知AB为⊙O的直径,C为⊙O上一点,CD与AB的延长线交于点D.
如图,已知AB为⊙O的直径,C为⊙O上一点,CD与AB的延长线交于点D.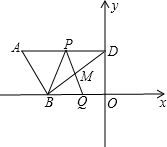 度向点D运动,到达点D后停止,点P、Q同时出发,BD与PQ相交于点M,设运动的时间为t秒.
度向点D运动,到达点D后停止,点P、Q同时出发,BD与PQ相交于点M,设运动的时间为t秒. 菱形,要求菱形的顶点均在格点上.
菱形,要求菱形的顶点均在格点上.