题目内容
 在△ABC中,AB=20cm,AC=16cm,点P从A点出发,沿AB方向以每秒4cm的速度向B点运动,同时点Q从C点出发,沿CA方向以每秒2cm的速度向A点运动,当P到达B点时,P、Q两点都停止运动,设运动时间为t秒,求t为何值时,以点A、P、Q为顶点的三角形与△ABC相似?
在△ABC中,AB=20cm,AC=16cm,点P从A点出发,沿AB方向以每秒4cm的速度向B点运动,同时点Q从C点出发,沿CA方向以每秒2cm的速度向A点运动,当P到达B点时,P、Q两点都停止运动,设运动时间为t秒,求t为何值时,以点A、P、Q为顶点的三角形与△ABC相似?考点:相似三角形的判定与性质
专题:动点型
分析:首先根据AB=20cm,点P从A点出发,沿AB方向以每秒4cm的速度向B点运动得到AP=4t,再根据AC=16cm,点Q从C点出发,沿CA方向以每秒2cm的速度向A点运动得到AQ=16-2t
然后分当△APQ∽△ABC时和当△AQP∽△ABC时两种情况求得t值即可.
然后分当△APQ∽△ABC时和当△AQP∽△ABC时两种情况求得t值即可.
解答:解:∵AB=20cm,点P从A点出发,沿AB方向以每秒4cm的速度向B点运动,
∴AP=4t,
∵AC=16cm,点Q从C点出发,沿CA方向以每秒2cm的速度向A点运动,
∴AQ=16-2t
(1)当△APQ∽△ABC时,
=
即:
=
解得:t=
(2)当△AQP∽△ABC时,
=
即:
=
解得:t=
∴当t=
或t=
秒时以点A、P、Q为顶点的三角形与△ABC相似.
∴AP=4t,
∵AC=16cm,点Q从C点出发,沿CA方向以每秒2cm的速度向A点运动,
∴AQ=16-2t
(1)当△APQ∽△ABC时,
| AP |
| AB |
| AQ |
| AC |
即:
| 4t |
| 16-2t |
| 20 |
| 16 |
解得:t=
| 40 |
| 13 |
(2)当△AQP∽△ABC时,
| AP |
| AC |
| AQ |
| AB |
即:
| 4t |
| 16 |
| 16-2t |
| 20 |
解得:t=
| 16 |
| 7 |
∴当t=
| 40 |
| 13 |
| 16 |
| 7 |
点评:本题考查了相似三角形的判定与性质,重点考查了分类思想的应用,本题的易错点是只考虑了一种情况.

练习册系列答案
相关题目
 用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,则第(6)个图形中黑色瓷砖的块数为( )
用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,则第(6)个图形中黑色瓷砖的块数为( )| A、19 | B、16 | C、18 | D、22 |
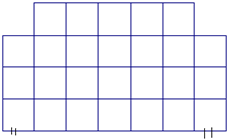 一展览馆有26间展室,图中每个方格代表一个展室,每相邻展室有门相同,出口、入口如图所示.问:能否找到一条从入口到出口的参观路线,使不重复不遗漏地走过每一间展室?
一展览馆有26间展室,图中每个方格代表一个展室,每相邻展室有门相同,出口、入口如图所示.问:能否找到一条从入口到出口的参观路线,使不重复不遗漏地走过每一间展室? 在面积为1的△ABC中,P为边BC上的中点,点Q在边AC上,且AQ=2QC,连接AP,BQ相交于点R,求:△ABR的面积?
在面积为1的△ABC中,P为边BC上的中点,点Q在边AC上,且AQ=2QC,连接AP,BQ相交于点R,求:△ABR的面积? 如图,平行四边形ABCD中,点E为AB边的中点,点F为BC边的三等分点,连接AF、DE相交于点G,则
如图,平行四边形ABCD中,点E为AB边的中点,点F为BC边的三等分点,连接AF、DE相交于点G,则