题目内容
11.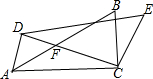 如图,△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕点C按顺时针方向旋转,旋转角为α(0°<α<90°),得到△DEC,设CD交AB于点F,连接AD,当α=40°时,AD=AF.
如图,△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕点C按顺时针方向旋转,旋转角为α(0°<α<90°),得到△DEC,设CD交AB于点F,连接AD,当α=40°时,AD=AF.
分析 由AD=AF,得出∠AFD=∠ADC,由旋转的性质得AC=CD,即∠ADC=∠CAD,由三角形的内角和定理得出∠ADC=$\frac{1}{2}$(180°-α),由三角形的外角性质得出∠AFD=∠BAC+α=30°+α,从而得出30°+α=$\frac{1}{2}$(180°-α),解方程即可得出结果.
解答 解:∵AD=AF,
∴∠AFD=∠ADC,
∵将△ABC绕点C按顺时针方向旋转,旋转角为α(0°<α<90°),得到△DEC,
∴AC=CD,∠ACD=α,
∴∠ADC=∠CAD,
∵在△ACD中,∠ADC=180°-∠CAD-α,
∴∠ADC=$\frac{1}{2}$(180°-α),
∵∠AFD=∠BAC+α=30°+α,
∴30°+α=$\frac{1}{2}$(180°-α),
解得:α=40°,
故答案为40°.
点评 本题考查了旋转的性质、等腰三角形的性质、三角形的内角和定理、三角形的外角性质等知识;熟练掌握旋转的性质,根据角的关系得出方程是解决问题的关键.

练习册系列答案
相关题目
14. 由六个小正方体搭成的几何体如图所示,则它的俯视图是( )
由六个小正方体搭成的几何体如图所示,则它的俯视图是( )
 由六个小正方体搭成的几何体如图所示,则它的俯视图是( )
由六个小正方体搭成的几何体如图所示,则它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
11.已知一次函数y=ax+b的图象经过一、二、三象限,且与x轴交于点(-2,0),则不等式ax>-b的解集为( )
| A. | x>-2 | B. | x<-2 | C. | x>2 | D. | x<2 |
16. 如图,△ABC绕点O顺时针旋转后,顶点A旋转到了点A′的位置,下列说法中,错误的是( )
如图,△ABC绕点O顺时针旋转后,顶点A旋转到了点A′的位置,下列说法中,错误的是( )
 如图,△ABC绕点O顺时针旋转后,顶点A旋转到了点A′的位置,下列说法中,错误的是( )
如图,△ABC绕点O顺时针旋转后,顶点A旋转到了点A′的位置,下列说法中,错误的是( )| A. | OA=OA′ | |
| B. | ∠AOA′是旋转角 | |
| C. | 作∠BOB′=∠AOA′,且OB′=OB,即可确定点B的对应点B′的位置 | |
| D. | 若点C的对应点为C′,则∠COC′=∠AOA′ |
3.要使(y2-ky+2y)(-y)的展开式中不含y2项,则k的值为( )
| A. | -2 | B. | 0 | C. | 2 | D. | 3 |
20.在Rt△ABC中,∠C=90°,AB=10,BC=6,则AC的长是( )
| A. | 8 | B. | 4$\sqrt{34}$ | C. | 64 | D. | 16 |
 如图所示,把一张长方形的纸条ABCD沿对角线BD将△BCD折成△BDF,DF交AB于E,若已知AE=2cm,∠BDC=30°,求纸条的长和宽各是6,2$\sqrt{3}$.
如图所示,把一张长方形的纸条ABCD沿对角线BD将△BCD折成△BDF,DF交AB于E,若已知AE=2cm,∠BDC=30°,求纸条的长和宽各是6,2$\sqrt{3}$.