Question

4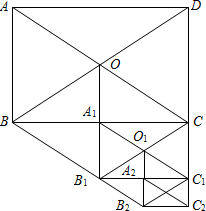．如图所示，在矩形ABCD中，AB=12，AC=20，两条对角线相交于点O．以OB、OC为邻边作第1个平行四边形OBB₁C，对角线相交于点A₁，再以A₁B₁、A₁C为邻边作第2个平行四边形A₁B₁C₁C，对角线相交于点O₁；再以O₁B₁、O₁C₁为邻边作第3个平行四边形O₁B₁B₂C₁…依此类推．则第6个平行四边形的面积为（　　）

• A． 6
• B． 3.75
• C． 15
• D． 12

Answer 1

分析 首先分别求得几个平行四边形的面积，即可得到规律：第n个平行四边形的面积为：$\frac{240}{{2}^{n}}$，继而求得答案．

解答 解：∵在矩形ABCD中，AB=12，BC=20，
∴S_矩形ABCD=AB•CD=240，OB=OC，
∵以OB，OC为邻边作第1个平行四边形OBB₁C，
∴平行四边形OBB₁C是菱形，
∴S_?OBB1C=$\frac{1}{2}$BC•OB₁=$\frac{1}{2}$×20×12=120，
S_?A1B1C1C=A₁C•A₁B₁=60，
∴第n个平行四边形的面积为：$\frac{240}{{2}^{n}}$，
∴第6个平行四边形的面积是：$\frac{240}{{2}^{6}}$=3.75．
故选：B．

点评 此题考查了平行四边形的性质以及矩形的性质．注意得到规律：第n个平行四边形的面积为$\frac{240}{{2}^{n}}$是关键．