题目内容
12.已知关于x,y的方程组$\left\{\begin{array}{l}{x+y=3}\\{ax-by=5}\end{array}\right.$与$\left\{\begin{array}{l}{bx-2ay=1}\\{x-7=y}\end{array}\right.$同解,求$\frac{b}{a}$的值.分析 根据题意得出方程组$\left\{\begin{array}{l}{x+y=3}\\{x-7=y}\end{array}\right.$,求出方程组的解,把x、y的值代入方程组$\left\{\begin{array}{l}{ax-by=5}\\{bx-2ay=1}\end{array}\right.$,得出关于ab的方程组,求出方程组的解即可.
解答 解:∵关于x,y的方程组$\left\{\begin{array}{l}{x+y=3}\\{ax-by=5}\end{array}\right.$与$\left\{\begin{array}{l}{bx-2ay=1}\\{x-7=y}\end{array}\right.$同解,
∴解方程组$\left\{\begin{array}{l}{x+y=3}\\{x-7=y}\end{array}\right.$,得:$\left\{\begin{array}{l}{x=5}\\{y=-2}\end{array}\right.$,
把x=5,y=-2代入方程组$\left\{\begin{array}{l}{ax-by=5}\\{bx-2ay=1}\end{array}\right.$,得:$\left\{\begin{array}{l}{5a+2b=5}\\{5b+4a=1}\end{array}\right.$,
解得:a=$\frac{23}{17}$,b=-$\frac{4}{5}$.
∴$\frac{b}{a}$=-$\frac{23}{15}$.
点评 本题考查了解二元一次方程组,二元一次方程组的解的应用,关键是能求出关于a、b的方程组.

练习册系列答案
相关题目
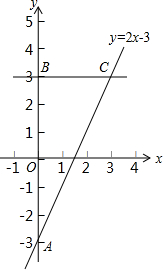 在平面直角坐标系xOy中,直线y=2x-3与y轴交于点A,点A与点B关于x轴对称,过点B作y轴的垂线l,直线l与直线y=2x-3交于点C.
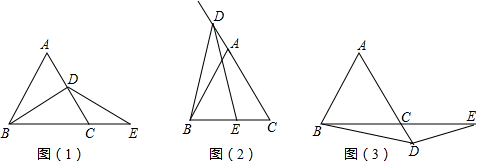
在平面直角坐标系xOy中,直线y=2x-3与y轴交于点A,点A与点B关于x轴对称,过点B作y轴的垂线l,直线l与直线y=2x-3交于点C.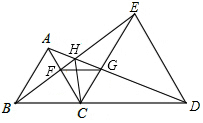 已知,点C是线段BD上一动点,分别以BC、CD为边向同侧作等边△ABC和等边三角形△CDE,如图所示.
已知,点C是线段BD上一动点,分别以BC、CD为边向同侧作等边△ABC和等边三角形△CDE,如图所示. 某中学为了解学生到校交通方式情况,随机抽取各年级部分学生就“上下学交通方式”进行问卷调查,调查分为“A:骑自行车;B:不行;C:坐公交车;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2),请根据图中的信息,解答下列问题:
某中学为了解学生到校交通方式情况,随机抽取各年级部分学生就“上下学交通方式”进行问卷调查,调查分为“A:骑自行车;B:不行;C:坐公交车;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2),请根据图中的信息,解答下列问题: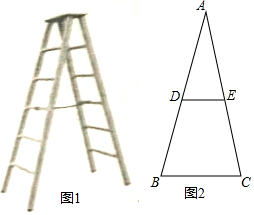 如图1所示的是由梯子AB和梯子AC搭成的“人字梯”,它的5个踩档把梯子等分成6份,梯子的第三踩档处有一条绑绳DE,将其抽象成图2,其中AB=AC=2米.
如图1所示的是由梯子AB和梯子AC搭成的“人字梯”,它的5个踩档把梯子等分成6份,梯子的第三踩档处有一条绑绳DE,将其抽象成图2,其中AB=AC=2米.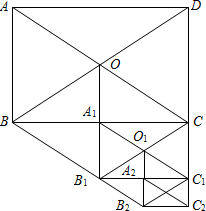 如图所示,在矩形ABCD中,AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.则第6个平行四边形的面积为( )
如图所示,在矩形ABCD中,AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.则第6个平行四边形的面积为( )