题目内容
13.某乡组织20辆汽车装运A、B、C三种苹果42吨到外地销售,按规定每辆车只装同一种苹果,且必须装满,每种苹果不少于2辆车.| 苹果品种 | A | B | C |
| 每辆汽车装载量/吨 | 2.2 | 2.1 | 2 |
| 每吨苹果获利/元 | 600 | 800 | 500 |
(2)设此次外销活动的利润为W元,求W与x之间的函数表达式及最大利润,并制定写出相应的车辆分配方案.
分析 (1)可根据运送A苹果的重量+运送B苹果的数量+运送C苹果的数量=42吨.来列关系式;
(2)总利润=A苹果的利润+B苹果的利润+C苹果的利润,然后根据(1)中得出的y,x的关系式代入上面的等量关系中,求出关于W、x的函数关系式,然后根据自变量的取值范围和函数关系式的性质来求出利润最大的方案.
解答 解:(1)由题意可知:2.2x+2.1y+2(20-x-y)=42,
即y=20-2x
$\left\{\begin{array}{l}{x≥2}\\{20-2x≥2}\\{20-x-(20-2x)≥2}\end{array}\right.$,
解得:2≤x≤9;
(2)由题意可得:w=2.2×6x+2.1×8(20-2x)+2(20-x-y)×5,
将y=20-2x代入上式可得:w=-10.4x+336由k=-10.4<0,可得w随x的增大而减小,
因此:当x=2时,w最大=315.2(百元)即用两辆车装A种苹果,16辆车装B种苹果,两辆车装C种苹果.
点评 本题考查了一次函数的实际应用,一次函数的综合应用题常出现于销售、收费、行程等实际问题当中,解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
4.某条抛物线向左平移1个单位,再向上平移2个单位后,所得到的方程是y=x2,那么原抛物线方程为( )
| A. | y=(x+1)2+2 | B. | y=(x+1)2-2 | C. | y=(x-1)2+2 | D. | y=(x-1)2-2 |
1.已知一个角的余角比它的补角的$\frac{1}{3}$还少10°,则这个角的度数是( )
| A. | 120° | B. | 90° | C. | 60° | D. | 30° |
2.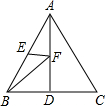 如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )
如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )
 如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )
如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )| A. | 7.5 | B. | 5 | C. | 4 | D. | 不能确定 |
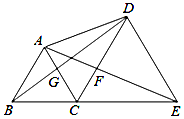 如图所示,点B、C、E在同一条直线上,AC=BC,CD=CE,∠ACB=∠DCE=60°.则下列结论:①△ACE≌△BCD;②CG=CF;③若连接GF,则GF∥BE;④△ADB≌△CEA.一定成立的有①②③.
如图所示,点B、C、E在同一条直线上,AC=BC,CD=CE,∠ACB=∠DCE=60°.则下列结论:①△ACE≌△BCD;②CG=CF;③若连接GF,则GF∥BE;④△ADB≌△CEA.一定成立的有①②③.