题目内容
2.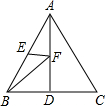 如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )
如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )| A. | 7.5 | B. | 5 | C. | 4 | D. | 不能确定 |
分析 过C作CE⊥AB于E,交AD于F,连接BF,则BF+EF最小,证△ADB≌△CEB得CE=AD=5,即BF+EF=5.
解答 解:过C作CE⊥AB于E,交AD于F,连接BF,则BF+EF最小(根据两点之间线段最短;点到直线垂直距离最短),由于C和B关于AD对称,则BF+EF=CF,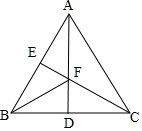
∵等边△ABC中,BD=CD,
∴AD⊥BC,
∴AD是BC的垂直平分线(三线合一),
∴C和B关于直线AD对称,
∴CF=BF,
即BF+EF=CF+EF=CE,
∵AD⊥BC,CE⊥AB,
∴∠ADB=∠CEB=90°,
在△ADB和△CEB中,
∵$\left\{\begin{array}{l}{∠ADB=∠CEB}\\{∠ABD=∠CBE}\\{AB=CB}\end{array}\right.$,
∴△ADB≌△CEB(AAS),
∴CE=AD=5,
即BF+EF=5,
故选:B.
点评 本题考查的是轴对称-最短路线问题,涉及到等边三角形的性质,轴对称的性质,等腰三角形的性质、全等三角形的判定和性质等知识点的综合运用.

练习册系列答案
相关题目
13.某乡组织20辆汽车装运A、B、C三种苹果42吨到外地销售,按规定每辆车只装同一种苹果,且必须装满,每种苹果不少于2辆车.
(1)设用x辆车装运A种苹果,用y辆车装运B种苹果.根据上表提供的信息,求y与x之间的函数表达式,并写出自变量x的取值范围;
(2)设此次外销活动的利润为W元,求W与x之间的函数表达式及最大利润,并制定写出相应的车辆分配方案.
| 苹果品种 | A | B | C |
| 每辆汽车装载量/吨 | 2.2 | 2.1 | 2 |
| 每吨苹果获利/元 | 600 | 800 | 500 |
(2)设此次外销活动的利润为W元,求W与x之间的函数表达式及最大利润,并制定写出相应的车辆分配方案.
17.若把分式$\frac{x+y}{2x+y}$中的x和y都扩大3倍,且x+y≠0,那么分式的值( )
| A. | 不变 | B. | 扩大3倍 | C. | 缩小3倍 | D. | 缩小6倍 |
11.下列说法正确的是( )
| A. | 三角形三条高都在三角形内 | |
| B. | 三角形的角平分线是射线 | |
| C. | 三角形的三条角平分线可能在三角形内,也可能在三角形外 | |
| D. | 三角形三条中线相交于一点 |
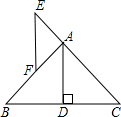 如图,在△ABC中,AB=AC,E在CA延长线上,AE=AF,AD是高,试判断EF与BC的位置关系,并说明理由.
如图,在△ABC中,AB=AC,E在CA延长线上,AE=AF,AD是高,试判断EF与BC的位置关系,并说明理由.